题目内容
已知函数f(x)=ax-x+b的零点x0∈(k,k+1)(k∈Z),其中常数a,b满足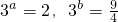 ,则k=________.
,则k=________.
1
分析:由已知条件求出a、b的值,代入函数f(x)=ax-x+b可得 函数f(x)=(log32)x-x+2-2log32,且函数是R上的减函数,根据函数的单调性和零点的性质进行求解.
解答:∵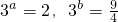 ,∴a=log32 b=
,∴a=log32 b=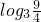 =2-2log32,
=2-2log32,
∴函数f(x)=(log32)x-x+2-2log32,且函数是R上的减函数,
而f(1)=2-2log32>0,f(2)=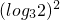 -2log32<0,
-2log32<0,
∴函数f(x)=(log32)x-x+2-2log32在(1,2)内有一个零点,
故k=1,
故答案为 1.
点评:本题主要考查了函数零点的判定定理以及指数与对数的互化,函数 f(x)=(log23)x+x-log32是增函数,单调函数最多只有一个零点,是解题的关键,属中档题.
分析:由已知条件求出a、b的值,代入函数f(x)=ax-x+b可得 函数f(x)=(log32)x-x+2-2log32,且函数是R上的减函数,根据函数的单调性和零点的性质进行求解.
解答:∵
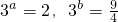 ,∴a=log32 b=
,∴a=log32 b=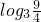 =2-2log32,
=2-2log32,∴函数f(x)=(log32)x-x+2-2log32,且函数是R上的减函数,
而f(1)=2-2log32>0,f(2)=
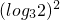 -2log32<0,
-2log32<0,∴函数f(x)=(log32)x-x+2-2log32在(1,2)内有一个零点,
故k=1,
故答案为 1.
点评:本题主要考查了函数零点的判定定理以及指数与对数的互化,函数 f(x)=(log23)x+x-log32是增函数,单调函数最多只有一个零点,是解题的关键,属中档题.

练习册系列答案
相关题目