题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{({x}^{2}-2ax){e}^{x},}&{x>0}\\{bx,}&{x≤0}\end{array}\right.$,g(x)=clnx+b,且x=$\sqrt{2}$是函数y=f(x)的极值点,直线l是函数y=f(x)的图象在点(2,f(2))处的切线.(1)求实数a的值和直线l的方程.
(2)若直线l与函数y=g(x)的图象相切于点P(x0,y0),x0∈[e-1,e],求实数b的取值范围.
分析 (1)求出x>0的f(x)的导数,由条件可得f′($\sqrt{2}$)=0,解得a=1,可得函数y=f(x)的图象在点(2,f(2))处的切线斜率和切点,由点斜式方程即可得到切线方程;
(2)求出g(x)的导数,求得g(x)在切点处的切线的斜率和切线方程,由两直线重合的条件可得b的解析式,记h(x0)=2e2(x0-x0lnx0-2),其中x0∈[e-1,e],运用导数求得单调区间,极值、最值,即可得到b的范围.
解答 解:(1)x>0时,f(x)=(x2-2ax)ex,
f′(x)=(2x-2a)ex+(x2-2ax)ex=[x2+2(1-a)x-2a]ex,
由已知,f′($\sqrt{2}$)=0,即有[2+2$\sqrt{2}$(1-a)-2a]${e}^{\sqrt{2}}$=0,
即 2+2$\sqrt{2}$(1-a)-2a=0,得a=1,
所以x>0时,f(x)=(x2-2x)ex,
f′(x)=(x2-2)ex,
即f(2)=0,f′(2)=2e2,
则函数f(x)的图象在点(2,f(2))处的切线l的方程为:y=2e2x-4e2;
(2)由于直线l与函数g(x)的图象相切于点P(x0,y0),x0∈[e-1,e],
即y0=clnx0+b,g′(x)=$\frac{c}{x}$
所以切线l的斜率为g′(x0)=$\frac{c}{{x}_{0}}$,
所以切线l的方程为y-y0=$\frac{c}{{x}_{0}}$(x-x0),
即l的方程为:y=$\frac{c}{{x}_{0}}$x-c+b+clnx0,
于是可得$\left\{\begin{array}{l}{\frac{c}{{x}_{0}}=2{e}^{2}}\\{-c+b+cln{x}_{0}=-4{e}^{2}}\end{array}\right.$⇒$\left\{\begin{array}{l}{c=2{e}^{2}{x}_{0}}\\{b=c-cln{x}_{0}-4{e}^{2}}\end{array}\right.$,
所以b=2e2(x0-x0lnx0-2)其中x0∈[e-1,e],
记h(x0)=2e2(x0-x0lnx0-2),其中x0∈[e-1,e],
h′(x0)=2e2(1-(lnx0+1))=-2e2lnx0,
令h′(x0)=0,得x0=1,
当x∈[e-1,1)时,h′(x0)>0,h(x0)递增,
当x∈(1,e]时,h′(x0)<0,h(x0)递减.
即有x0=1处b取得极大值,也为最大值,且为-2e2,
当x0=e-1时,b=4e-4e2,当x0=e时,b=-4e2,
即有b的最小值为-4e2,
则b的取值范围是[-4e2,-2e2].
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,主要考查导数的几何意义和直线方程的运用,正确求导和构造函数以及运用直线重合的条件是解题的关键.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案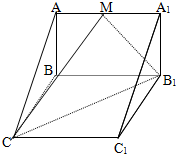 如图,在直三棱锥ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点且B1M与平面ACC1所成角为30°,确定M的位置.
如图,在直三棱锥ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点且B1M与平面ACC1所成角为30°,确定M的位置.