题目内容
5.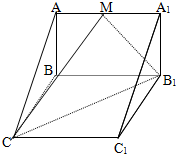 如图,在直三棱锥ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点且B1M与平面ACC1所成角为30°,确定M的位置.
如图,在直三棱锥ABC-A1B1C1中,AB=BC=1,∠ABC=90°,AA1=2,M为棱AA1上一点且B1M与平面ACC1所成角为30°,确定M的位置.
分析 以BC,BB1,BA为x,y,z轴建立空间坐标系,确定相关的点的坐标,求出平面ACC1的法向量$\overrightarrow{n}$=(x1,y1,z1),根据B1M与平面ACC1所成角为30°,得出$\overrightarrow{{B}_{1}M}$与$\overrightarrow{n}$成角为60°,
根据向量的数量积得出点的位置.
解答 解: 以BC,BB1,BA为x,y,z轴建立空间坐标系,
以BC,BB1,BA为x,y,z轴建立空间坐标系,
∵AB=BC=1,∠ABC=90°,AA1=2,
∴B(0,0,0),A(0,0,1),C(1,0,0),B1(0,2,0),M(0,y,1),C1(1,2,0)
∴$\overrightarrow{{B}_{1}M}$=(0,y-2,1),$\overrightarrow{AC}$=(1,0,-1),$\overrightarrow{C{C}_{1}}$=(0,2,0),
∵平面ACC1的法向量$\overrightarrow{n}$=(x1,y1,z1),
∴$\left\{\begin{array}{l}{{x}_{1}-{z}_{1}=0}\\{2{y}_{1}=0}\end{array}\right.$
令x1=1,y1=0,z1=1,
∴$\overrightarrow{n}$=(1.0,1),
∵B1M与平面ACC1所成角为30°
∴$\overrightarrow{{B}_{1}M}$与$\overrightarrow{n}$成角为60°,
∴根据向量的数量积得出:1=$\sqrt{2}×\frac{1}{2}×\sqrt{(y-2)^{2}+1}$,0≤y≤2
解得:y=3(舍去),y=1,
∴M(0,1,1)
故M是AA1的中点.
点评 本题考查了空间直线平面垂直,所成的角的问题,建立坐标系,运用向量的数量积求解,计算要仔细认真,题目不难,容易出错.

 阅读快车系列答案
阅读快车系列答案| A. | y=2x-2 | B. | y=-2x+2 | C. | y=x-1 | D. | y=-x+1 |
| A. | x2f(lnx1)<x1f(lnx2) | B. | x2f(lnx1)>x2f(lnx2) | C. | x1f(lnx1)>x2f(lnx2) | D. | x1f(lnx1)<x2f(lnx2) |
 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,A1A=2,点E是棱CC1的中点
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,A1A=2,点E是棱CC1的中点 如图,已知四棱锥P-ABCD的底面是菱形,PB=PD,E为PA的中点.
如图,已知四棱锥P-ABCD的底面是菱形,PB=PD,E为PA的中点.