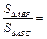题目内容
已知点G是△ABC的重心，
=λ
+μ
(λ，μ∈R)，那么λ+μ=______；若∠A=120°，
•
=-2，则|
|的最小值是______．
| AG |
| AB |
| AC |
| AB |
| AC |
| AG |
∵点G是△ABC的重心
∴点G分中线为
∴
=
×
（
+
）=
（
+
）
∵
=λ
+μ
(λ，μ∈R)
∴λ=
，μ=
∴λ+μ=
故答案为
设|
|=b，|
|=c
∵∠A=120°，
•
=-2
∴bccos120°=-2即bc=4
∵
=
（
+
）
∴|
|2=
(
2+2
•
+
2)=
（b2+c2-4）≥
(2bc-4)=
∴|
|=
当且仅当b=c时取等号．
故答案为∴|
|的最小值为
∴点G分中线为
| 1 |
| 2 |
∴
| AG |
| 2 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
| AC |
∵
| AG |
| AB |
| AC |
∴λ=
| 1 |
| 3 |
| 1 |
| 3 |
∴λ+μ=
| 2 |
| 3 |
故答案为
| 2 |
| 3 |
设|
| AC |
| AB |
∵∠A=120°，
| AB |
| AC |
∴bccos120°=-2即bc=4
∵
| AG |
| 1 |
| 3 |
| AB |
| AC |
∴|
| AG |
| 1 |
| 9 |
| AB |
| AB |
| AC |
| AC |
| 1 |
| 9 |
| 1 |
| 9 |
| 4 |
| 9 |
∴|
| AG |
| 2 |
| 3 |
故答案为∴|
| AG |
| 2 |
| 3 |
练习册系列答案
相关题目
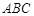中, 
,
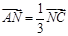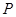是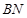
上的一点,若
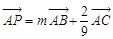,则实数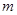
的值为( )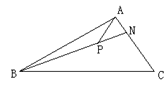 
，O为△ABC的外心，P为劣弧AC上一动点，且
＝x
＋y
(x，y∈R)，则x＋y的取值范围为________．
