题目内容
如图所示,把两块斜边长相等的直角三角板拼在一起,若
=x
+y
,则x=______,y=______.

| AD |
| AB |
| AC |

解∵
=x
+y
,又
=
+
,∴
+
=x
+y
,
∴
=(x-1)
+y
.
又∵
⊥
,∴
•
=(x-1)
2.
设|
|=1,则由题意知:|
|=|
|=
.
又∵∠BED=60°,∴|
|=
,显然
与
的夹角为45°.
∴由
•
=(x-1)
2得
×1×cos45°=(x-1)×1,∴x=
+1.
同理,在
=(x-1)
+y
中,两边同时乘以
,
由数量积公式可得:y=
,故答案为:1+
,
.
| AD |
| AB |
| AC |
| AD |
| AB |
| BD |
| AB |
| BD |
| AB |
| AC |
∴
| BD |
| AB |
| AC |
又∵
| AC |
| AB |
| BD |
| AB |
| AB |
设|
| AB |
| DE |
| BC |
| 2 |
又∵∠BED=60°,∴|
| BD |
| ||
| 2 |
| BD |
| AB |
∴由
| BD |
| AB |
| AB |
| ||
| 2 |
| ||
| 2 |
同理,在
| BD |
| AB |
| AC |
| AC |
由数量积公式可得:y=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 中,已知
中,已知 ,
, ,
,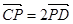 .
. 的值;
的值; ,求
,求 与
与 夹角的余弦值.
夹角的余弦值. ,
, ,点A
,点A .
. 满足
满足 ,求
,求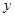 和
和 的值.
的值. 所成的比是
所成的比是 ,则点A分
,则点A分 所成的比是____________.
所成的比是____________. ,
, ,则
,则 ______________。
______________。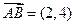 ,
,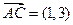 ,则
,则 ( )
( )