题目内容
某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回.
(Ⅰ)设第一次训练时取到的新球个数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)求第二次训练时恰好取到一个新球的概率.
(Ⅰ)设第一次训练时取到的新球个数为
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)求第二次训练时恰好取到一个新球的概率.
(Ⅰ)
 的数学期望为
的数学期望为 (Ⅱ)
(Ⅱ)
 | 0 | 1 | 2 |
 |  |  |  |
 的数学期望为
的数学期望为 (Ⅱ)
(Ⅱ)
试题分析:(1)
 的所有可能取值为0,1,2.
的所有可能取值为0,1,2. 设“第一次训练时取到
 个新球(即
个新球(即 )”为事件
)”为事件 (
( 0,1,2).因为集训前共有6个篮球,其中3个是新球,3个是旧球,所以
0,1,2).因为集训前共有6个篮球,其中3个是新球,3个是旧球,所以
 ,
,  .
. 所以
 的分布列为
的分布列为 | 0 | 1 | 2 |
 |  |  |  |
 的数学期望为
的数学期望为 .
. (2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件
 .
.则“第二次训练时恰好取到一个新球”就是事件
 .
.而事件
 、
、 、
、 互斥,
互斥,所以,
 .
.由条件概率公式,得
 ,
,  ,
, 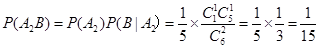 .
. 所以,第二次训练时恰好取到一个新球的概率为
 .
. 点评:求分布列的步骤:找到随机变量可以取得值,求出各值对应的概率,汇总成分布列,第二问考查的是条件概率:在事件A发生的条件下事件B发生的概率为


练习册系列答案
相关题目
 粒大小、形状相同但颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率
粒大小、形状相同但颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率 与倒出偶数粒玻璃球的概率
与倒出偶数粒玻璃球的概率 的(大小或相等)关系是 。
的(大小或相等)关系是 。 位学生,每次活动均需该系
位学生,每次活动均需该系 位学生参加(
位学生参加(
 取得最大值的整数
取得最大值的整数 .
. ,由于发扬团队精神,此题能解出的概率是 .
,由于发扬团队精神,此题能解出的概率是 . ,则
,则 的值为_____.
的值为_____.
 、
、 、
、 ,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为 .
.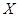 ,求
,求 .
. ,则甲回家途中遇红灯次数的期望为( )
,则甲回家途中遇红灯次数的期望为( )


