题目内容
已知y=f(x)是定义在(-∞,+∞)上的奇函数，且在［0,+∞)上为增函数.(1)求证：y=f(x)在(-∞,0]上是增函数；
(2)如果f(
)=1，解不等式-1＜f(2x+1)≤0.
(1)证明：略.
(2)解析：∵f(x)是定义在（-∞,+∞）上的奇函数，∴f(0)=0.
∵f()=1,
∴f(-
)=-1,
∴-1＜f(2x+1)≤0
f(-
)＜f(2x+1)≤f(0).
∵f(x)在［0,+∞）上为增函数，
∴f(x)在(-∞，0]上也为增函数，
∴
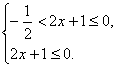
解得 -
＜x≤-
.
练习册系列答案
小学课时特训系列答案
相关题目
的定义域为(0，＋∞)，且f(2)＝2＋
．设点P是函数图象上的任意一点，过点P分别作直线y＝x和y轴的垂线，垂足分别为M、N．
的定义域为(0，＋∞)，且f(2)＝2＋
，设点P是函数图象上的任意一点，过点P分别作直线y＝x和y轴的垂线，垂足分别为M，N．