题目内容
已知函数 的图象过点
的图象过点 ,且在[-2,1)内单调递减,在[1,+∞)上单调递增.
,且在[-2,1)内单调递减,在[1,+∞)上单调递增.(1)求f(x)的解析式;
(2)若对于任意的x1,x2∈[m,m+3](m≥0),不等式
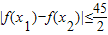 恒成立,试问这样的m是否存在.若存在,请求出m的范围,若不存在,说明理由.
恒成立,试问这样的m是否存在.若存在,请求出m的范围,若不存在,说明理由.
【答案】分析:(1)求导函数,利用[-2,1)内单调递减,在[1,+∞)上单调递增,可确定sinθ=1,a= ,再由f(1)=
,再由f(1)=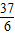 ,即可求得f(x)的解析式;
,即可求得f(x)的解析式;
(2)由导函数,确定f(x)的单调性.再进行分类讨论,利用|f(x1)-f(x2)|≤f(x)max-f(x)min,即可求得结论.
解答:解:(1)求导函数,可得f′(x)=3ax2+xsinθ-2,
由题设可知: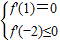 ,即
,即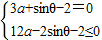 ,∴sinθ≥1,∴sinθ=1.
,∴sinθ≥1,∴sinθ=1.
从而a= ,
,
∴f(x)= x3+
x3+ x2-2x+c,而又由f(1)=
x2-2x+c,而又由f(1)=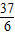 得c=
得c=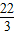 .
.
∴f(x)=3x3+2x2-2x+3即为所求.
(2)由f′(x)=x2+x-2=(x+2)(x-1),
∴f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数.
①当m>1时,f(x)在[m,m+3]上递增,故f(x)max=f(m+3),f(x)min=f(m)
由f(m+3)-f(m)=3(m+3)3+2(m+3)2-2(m+3)-3m3-2m2+2m=3m2+12m+2≤2,
得-5≤m≤1.这与条件矛盾,故 不存在.
②当0≤m≤1时,f(x)在[m,1]上递增,在[1,m+3]上递增
∴f(x)min=f(1),f(x)max=max{ f(m),f(m+3)},
又f(m+3)-f(m)=3m2+12m+2=3(m+2)2-2>0(0≤m≤1)
∴f(x)max=f(m+3)
∴|f(x1)-f(x2)|≤f(x)max-f(x)min=f(m+3)-f(1)≤f(4)-f(1)=2恒成立.
故当0≤m≤1时,原不等式恒成立.
综上,存在m∈[0,1]合题意
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,解题的关键是利用|f(x1)-f(x2)|≤f(x)max-f(x)min,属于中档题.
 ,再由f(1)=
,再由f(1)=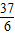 ,即可求得f(x)的解析式;
,即可求得f(x)的解析式;(2)由导函数,确定f(x)的单调性.再进行分类讨论,利用|f(x1)-f(x2)|≤f(x)max-f(x)min,即可求得结论.
解答:解:(1)求导函数,可得f′(x)=3ax2+xsinθ-2,
由题设可知:
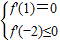 ,即
,即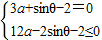 ,∴sinθ≥1,∴sinθ=1.
,∴sinθ≥1,∴sinθ=1.从而a=
 ,
,∴f(x)=
 x3+
x3+ x2-2x+c,而又由f(1)=
x2-2x+c,而又由f(1)=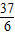 得c=
得c=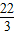 .
.∴f(x)=3x3+2x2-2x+3即为所求.
(2)由f′(x)=x2+x-2=(x+2)(x-1),
∴f(x)在(-∞,-2)及(1,+∞)上均为增函数,在(-2,1)上为减函数.
①当m>1时,f(x)在[m,m+3]上递增,故f(x)max=f(m+3),f(x)min=f(m)
由f(m+3)-f(m)=3(m+3)3+2(m+3)2-2(m+3)-3m3-2m2+2m=3m2+12m+2≤2,
得-5≤m≤1.这与条件矛盾,故 不存在.
②当0≤m≤1时,f(x)在[m,1]上递增,在[1,m+3]上递增
∴f(x)min=f(1),f(x)max=max{ f(m),f(m+3)},
又f(m+3)-f(m)=3m2+12m+2=3(m+2)2-2>0(0≤m≤1)
∴f(x)max=f(m+3)
∴|f(x1)-f(x2)|≤f(x)max-f(x)min=f(m+3)-f(1)≤f(4)-f(1)=2恒成立.
故当0≤m≤1时,原不等式恒成立.
综上,存在m∈[0,1]合题意
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,解题的关键是利用|f(x1)-f(x2)|≤f(x)max-f(x)min,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 的图象过点A(3,7),则此函的最小值是 .
的图象过点A(3,7),则此函的最小值是 . 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
. 的解析式;
的解析式; ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值; 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围. 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数