题目内容
已知双曲线的中心在原点,以两条坐标轴为对称轴,离心率是![]() ,两准线间的距离大于
,两准线间的距离大于![]() ,且双曲线上动点P到A(2,0)的最近距离为1。
,且双曲线上动点P到A(2,0)的最近距离为1。
(Ⅰ)求证:该双曲线的焦点不在y轴上;
(Ⅱ)求双曲线的方程;
(Ⅲ)如果斜率为k的直线L过点M(0,3),与该双曲线交于A、B两点,若![]() ,试用l表示k2,并求当
,试用l表示k2,并求当![]() 时,k的取值范围。
时,k的取值范围。
证明(Ⅰ):设双曲线的实轴长为2a,虚轴长为2b,焦距为2c,
由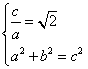 ,得c=
,得c=![]() a,a=b,
a,a=b,
∴双曲线的渐近线方程为y=±x。
若双曲线的焦点在y轴上,则双曲线上任一点到点A(2,0)的距离大于点A到渐近线的距离,而点A到渐近线的距离d=![]() >1,这与“双曲线上动点P到A(2,0)的最近距离为1”矛盾。所以双曲线的焦点不在y轴上。
>1,这与“双曲线上动点P到A(2,0)的最近距离为1”矛盾。所以双曲线的焦点不在y轴上。
解(Ⅱ):由(Ⅰ)知,双曲线的焦点在x轴上,
设双曲线的方程为x2-y2=a2,P(x0,y0),则![]() ,
,
|PA|2=![]() =
=![]() =
=![]() ,
,
a>1.当点P到A的距离最小时,x0³a,又由![]() 得a>1,
得a>1,
所以,当x0=a时,|PA|2有最小值,即2(a-1)2+2-a2=(a-2)2=1,
∴a=3,所以,双曲线的方程为x2-y2=9
解(Ⅲ):设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2)
∵![]() ,
,
∴(-x1,3-y1)=l(x2,y2-3) , ∴x1=-lx2(x1x2<0) ①,
由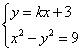 消去y得,(1-k2)x2-6kx-18=0,
消去y得,(1-k2)x2-6kx-18=0,
x1+x2=![]() ②, x1x2=
②, x1x2=![]() <0 ③
<0 ③
将①分别代入②、③得,(1-l)x2=![]() ④ lx22=
④ lx22=![]() ⑤
⑤
④2¸⑤并整理得,![]() (l>0)
(l>0)
令f(l)=![]() ,则
,则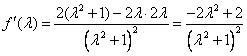
令![]() ,得l=1;令
,得l=1;令![]() ,得0<l<1;令
,得0<l<1;令![]() ,得l>1
,得l>1
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,∴
,∴![]()
∴![]() ,∴
,∴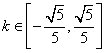

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目