题目内容
已知直线l0:x-y+2=0和圆C:x2+y2-8x+8y+14=0,设与直线l0和圆C都相切且半径最小的圆为圆M,直线l与圆M相交于A,B两点,且圆M上存在点P,使得
=
+
=λ
,其中
=(1 , 3).
(1)求圆M的标准方程;
(2)求直线l的方程及相应的点P坐标.
| OP |
| OA |
| OB |
| a |
| a |
(1)求圆M的标准方程;
(2)求直线l的方程及相应的点P坐标.
分析:(1)化简圆C为标准方程(x-4)2+(y+4)2=18,求出圆心C(4,-4),半径r0=3
,求出圆心C到直线l0的距离d0,推出⊙M的半径r,利用⊙M的圆心M在经过点C(4,-4),与l0的垂直的直线上,设出圆心M(x0,-x0),则由|MC|=r+r0,解得M坐标,求出M的标准方程.
(2)由
=
+
=λ
=(λ,3λ),求出P的坐标,求出kAB,设直线l:y=-
x+b,利用圆心M(0,0)到直线l的距离,求出P,得到直线l的方程.
| 2 |
(2)由
| OP |
| OA |
| OB |
| a |
| 1 |
| 3 |
解答:解:(1)∵圆C:x2+y2-8x+8y+14=0,即(x-4)2+(y+4)2=18,
所以圆心C(4,-4),半径r0=3
,圆心C到直线l0的距离d0=
=5
,
则⊙M的半径r=
=
,
⊙M的圆心M在经过点C(4,-4),与l0的垂直的直线上,即在直线y=-x上
设圆心M(x0,-x0),则由|MC|=r+r0=4
,解得M(0,0)或(8,-8)
其中只有M(0,0)满足到直线l0的距离为半径r=
,即符合题意
⊙M的标准方程为:x2+y2=2.
(2)由
=
+
=λ
=(λ,3λ),即点P(l,3l)代入⊙M:x2+y2=2,,得l=
,
P(
,
)或(-
,-
),且kOP=3,
∵
=
+
,且|
|=|
|+|
|=r,
∴
⊥
,kAB=-
=-
,
设直线l:y=-
x+b,即x+3y-3b=0,
圆心M(0,0)到直线l的距离d′=
=
=
,
解得3b=
则当点P(
,
)时,l:x+3y-
=0;
当点P(-
,-
)时,l:x+3y+
=0.
所以圆心C(4,-4),半径r0=3
| 2 |
| |4+4+2| | ||
|
| 2 |
则⊙M的半径r=
| d0-r |
| 2 |
| 2 |
⊙M的圆心M在经过点C(4,-4),与l0的垂直的直线上,即在直线y=-x上
设圆心M(x0,-x0),则由|MC|=r+r0=4
| 2 |
其中只有M(0,0)满足到直线l0的距离为半径r=
| 2 |
⊙M的标准方程为:x2+y2=2.
(2)由
| OP |
| OA |
| OB |
| a |
| ||
| 5 |
P(
| ||
| 5 |
3
| ||
| 5 |
| ||
| 5 |
3
| ||
| 5 |
∵
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
∴
| OP |
| AB |
| 1 |
| kOP |
| 1 |
| 3 |
设直线l:y=-
| 1 |
| 3 |
圆心M(0,0)到直线l的距离d′=
| |-3b| | ||
|
| r |
| 2 |
| ||
| 2 |
解得3b=
| 5 |
| ||
| 5 |
3
| ||
| 5 |
| 5 |
当点P(-
| ||
| 5 |
3
| ||
| 5 |
| 5 |
点评:本题考查直线与圆的方程的综合应用,圆心坐标的求法,圆心到直线的距离的求法,考查计算能力,转化思想.

练习册系列答案
相关题目
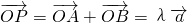 ,其中
,其中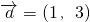 .
.