题目内容
对实数a和b,定义运算“?”:a?b= ,设函数f(x)=(x2-2)?(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
,设函数f(x)=(x2-2)?(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
A.(-∞,-2]∪ | B. |
C. | D.(-∞,-2]∪ |
D
解析试题分析:因为a?b= ,所以f(x)=(x2-2)?(x-x2)
,所以f(x)=(x2-2)?(x-x2) ,画出函数f(x)的图像,由图像可知实数c的取值范围是(-∞,-2]∪
,画出函数f(x)的图像,由图像可知实数c的取值范围是(-∞,-2]∪ 。
。
考点:分段函数;分段函数的图像;不等式的解法。
点评:本题主要考查数形结合思想,考查了学生用图的能力。分段函数的图像要分段画。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
已知定义在 上的函数
上的函数 满足
满足 ,且
,且 的导函数
的导函数 则不等式
则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
已知函数 ,满足
,满足 ,则
,则 的值为( )
的值为( )
A. | B. | C.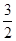 | D.1 |
已知函数 则
则 的值为( )
的值为( )
| A.4 | B.6 | C.8 | D.11 |
已知函数 ,且
,且 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C. 或 或 | D. 或 或 或 或 |
设 ,则
,则 的大小关系是( )
的大小关系是( )
| A.a>c>b | B.a>b>c |
| C.c>a>b | D.b>c>a |
已知定义在 上的函数
上的函数 满足
满足 ,且
,且
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 等于( )
等于( )
| A.4 | B.6 | C.5 | D.7 |
若指数函数 在
在 上是减函数,那么( )
上是减函数,那么( )
A.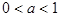 | B. | C.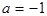 | D. |
 ,函数
,函数 与
与 的图像可能是( )
的图像可能是( )