题目内容
已知椭圆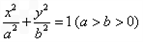 的左焦点为
的左焦点为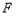
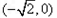 ,离心率e=
,离心率e=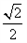 ,M、N是椭圆上的动点。
,M、N是椭圆上的动点。
(Ⅰ)求椭圆标准方程;
(Ⅱ)设动点P满足: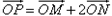 ,直线OM与ON的斜率之积为
,直线OM与ON的斜率之积为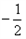 ,问:是否存在定点
,问:是否存在定点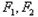 ,使得
,使得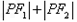 为定值?,若存在,求出
为定值?,若存在,求出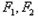 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
(Ⅲ)若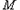 在第一象限,且点
在第一象限,且点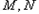 关于原点对称,点
关于原点对称,点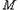 在
在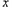 轴上的射影为
轴上的射影为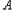 ,连接
,连接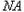 并延长交椭圆于点
并延长交椭圆于点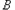 ,证明:
,证明: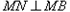 ;
;
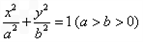 的左焦点为
的左焦点为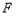
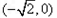 ,离心率e=
,离心率e=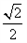 ,M、N是椭圆上的动点。
,M、N是椭圆上的动点。(Ⅰ)求椭圆标准方程;
(Ⅱ)设动点P满足:
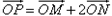 ,直线OM与ON的斜率之积为
,直线OM与ON的斜率之积为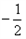 ,问:是否存在定点
,问:是否存在定点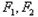 ,使得
,使得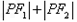 为定值?,若存在,求出
为定值?,若存在,求出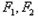 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。(Ⅲ)若
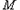 在第一象限,且点
在第一象限,且点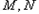 关于原点对称,点
关于原点对称,点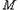 在
在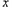 轴上的射影为
轴上的射影为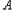 ,连接
,连接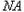 并延长交椭圆于点
并延长交椭圆于点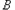 ,证明:
,证明: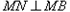 ;
;解:(Ⅰ)由题设可知: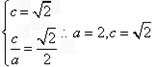
故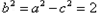
故椭圆的标准方程为: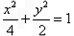
(Ⅱ)设 ,由
,由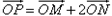 可得:
可得:
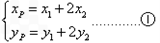
由直线OM与ON的斜率之积为 可得:
可得:
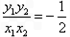 ,即
,即
由①②可得: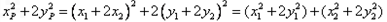
M、N是椭圆上,故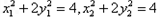
故 ,即
,即
由椭圆定义可知存在两个定点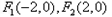 ,使得动点P到两定点距离和为定值
,使得动点P到两定点距离和为定值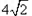 ;
;
(Ⅲ)设 由题设可知
由题设可知
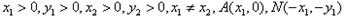
由题设可知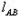 斜率存在且满足
斜率存在且满足
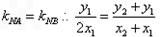 …………③
…………③

将③代入④可得: ……⑤
……⑤
点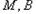 在椭圆
在椭圆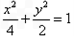 ,
,
故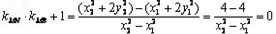
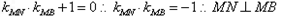
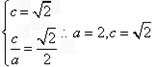
故
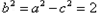
故椭圆的标准方程为:
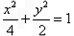
(Ⅱ)设
 ,由
,由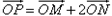 可得:
可得: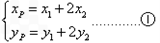
由直线OM与ON的斜率之积为
 可得:
可得: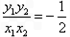 ,即
,即
由①②可得:
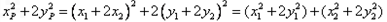
M、N是椭圆上,故
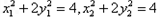
故
 ,即
,即
由椭圆定义可知存在两个定点
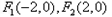 ,使得动点P到两定点距离和为定值
,使得动点P到两定点距离和为定值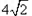 ;
;(Ⅲ)设
 由题设可知
由题设可知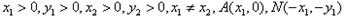
由题设可知
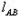 斜率存在且满足
斜率存在且满足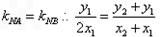 …………③
…………③ 
将③代入④可得:
 ……⑤
……⑤点
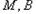 在椭圆
在椭圆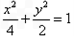 ,
,故
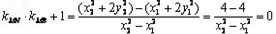
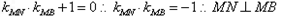

练习册系列答案
相关题目
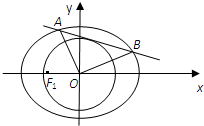 已知椭圆C:
已知椭圆C: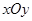 中,已知椭圆
中,已知椭圆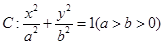 的左焦点为
的左焦点为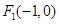 ,且椭圆
,且椭圆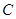 的离心率
的离心率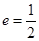 .
.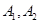 ,
,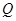 是椭圆
是椭圆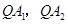 分别交
分别交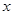 轴于点
轴于点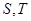 ,证明:
,证明: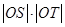 为定值,并求出该定值;
为定值,并求出该定值;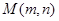 ,使得直线
,使得直线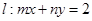 与圆
与圆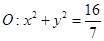 相交于不同的两点
相交于不同的两点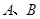 ,且
,且 的面积最大?若存在,求出点
的面积最大?若存在,求出点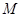 的坐标及对应的
的坐标及对应的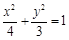 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率;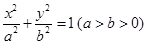 的左焦点为
的左焦点为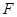
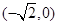 ,离心率e=
,离心率e=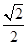 ,M、N是椭圆上的动
,M、N是椭圆上的动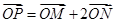 ,直线OM与ON的斜率之积为
,直线OM与ON的斜率之积为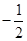 ,问:是否存在定点
,问:是否存在定点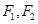 ,
,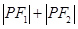 为定值?,若存在,求出
为定值?,若存在,求出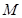 在第一象限,且点
在第一象限,且点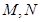 关于原点对称,点
关于原点对称,点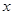 轴上的射影为
轴上的射影为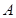 ,连接
,连接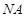 并延长
并延长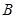 ,证明:
,证明: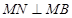 ;
; 的左焦点为
的左焦点为 ,右顶点为
,右顶点为 ,点
,点 在椭圆上,且
在椭圆上,且 轴, 直线
轴, 直线 交
交 轴于点
轴于点 .若
.若 ,则椭圆的离心率是( )w.w.w.七彩教育网.c.o.m
,则椭圆的离心率是( )w.w.w.七彩教育网.c.o.m  B.
B. C.
C. D.
D.