题目内容
如图,某污水处理厂要在一正方形污水处理池 内修建一个三角形隔离区以投放净化物质,其形状为三角形
内修建一个三角形隔离区以投放净化物质,其形状为三角形 ,其中
,其中 位于边
位于边 上,
上, 位于边
位于边 上.已知
上.已知 米,
米,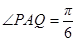 ,设
,设 ,记
,记 ,当
,当 越大,则污水净化效果越好.
越大,则污水净化效果越好.
(1)求 关于的函数解析式,并求定义域;
关于的函数解析式,并求定义域;
(2)求 最大值,并指出等号成立条件?
最大值,并指出等号成立条件?
(1) ;(2)
;(2) 时,
时, 取得最大值3.
取得最大值3.
解析试题分析:(1)我们只要求出两边 ,就能求出
,就能求出 的面积,从图中易知在
的面积,从图中易知在 中,
中, ,在
,在 中,
中, ,由此
,由此
 ;
;
(2)由 表达式可知,要求其最大值,必须把它转化为一个三角函数,且为一次的函数形式,即化为
表达式可知,要求其最大值,必须把它转化为一个三角函数,且为一次的函数形式,即化为 形式,
形式,

 ,这样问题可利用正弦函数
,这样问题可利用正弦函数 的性质解决.
的性质解决.
试题解析:(1) ,
,
 +2分
+2分
 +4分
+4分 +6分
+6分 ,
, +7分
+7分
(2) +11分
+11分 当
当 时,即
时,即 时
时 +13分
+13分
答 :当 时,
时, 的最大值为3. +14分
的最大值为3. +14分
考点:(1)三角形的面积;(2)三角函数的最值问题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,且
,且 .
. ,且
,且 ,求证:
,求证: .
. ,
, ,
,  .
. 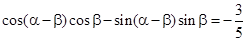 ,
, ,求
,求 的值.
的值. ,且
,且 .
. ;
; .
. ,则
,则 的值为
的值为  cos
cos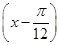 ,x∈R.
,x∈R. 的值;
的值; ,θ∈
,θ∈ ,求f
,求f .
. sin Ccos C-cos2C=
sin Ccos C-cos2C= ,且c=3.
,且c=3.