题目内容
在平面直角坐标系中,A(1,-2),B(-3,-4),O为坐标原点.
(Ⅰ)求 ;
;
(Ⅱ)若点P在直线AB上,且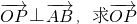 的坐标.
的坐标.
解:(Ⅰ) (5分)
(5分)
(Ⅱ)设P(m,n)
∵P在AB上,
∴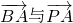 共线
共线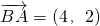
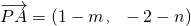
∴4•(-2-n)-2(1-m)=0
即2n-m+5=0①(9分)
又∵
∴(m,n)•(-4,-2)=0
∴2m+n=0②(12分)
由①②解得m=1,n=-2即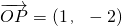 (14分)
(14分)
分析:(I)直接利用向量数量积的坐标公式可求
(II)先设P(m,n)由P在AB上,可得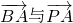 共线,根据向量共线的坐标表示可得m,n的关系;
共线,根据向量共线的坐标表示可得m,n的关系;
再由 ,可得
,可得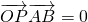 ,根据向量的数量积的坐标表示可得m,n的关系,从而可求m,n
,根据向量的数量积的坐标表示可得m,n的关系,从而可求m,n
点评:本题主要考查了平面向量的平行与垂直的坐标表示,要注意两者的不同,若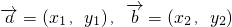 则
则 ?x1x2+y1y2=0;
?x1x2+y1y2=0;  ?x1y2-x2y1=0
?x1y2-x2y1=0
 (5分)
(5分)(Ⅱ)设P(m,n)
∵P在AB上,
∴
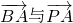 共线
共线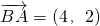
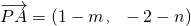
∴4•(-2-n)-2(1-m)=0
即2n-m+5=0①(9分)
又∵

∴(m,n)•(-4,-2)=0
∴2m+n=0②(12分)
由①②解得m=1,n=-2即
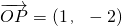 (14分)
(14分)分析:(I)直接利用向量数量积的坐标公式可求
(II)先设P(m,n)由P在AB上,可得
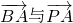 共线,根据向量共线的坐标表示可得m,n的关系;
共线,根据向量共线的坐标表示可得m,n的关系;再由
 ,可得
,可得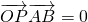 ,根据向量的数量积的坐标表示可得m,n的关系,从而可求m,n
,根据向量的数量积的坐标表示可得m,n的关系,从而可求m,n点评:本题主要考查了平面向量的平行与垂直的坐标表示,要注意两者的不同,若
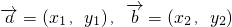 则
则 ?x1x2+y1y2=0;
?x1x2+y1y2=0;  ?x1y2-x2y1=0
?x1y2-x2y1=0 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目