题目内容
已知函数f(x)= ax2+2x,g(x)=lnx,
ax2+2x,g(x)=lnx,
(1)如果函数y=f(x)在[1,+∞)上是单调增函数,求a的取值范围;
(2)是否存在实数a>0,使得方程 =f′(x)-(2a+1)在区间
=f′(x)-(2a+1)在区间 内有且只有两个不相等的实数根?若存在,请求出a的取值范围;若不存在,请说明理由.
内有且只有两个不相等的实数根?若存在,请求出a的取值范围;若不存在,请说明理由.
 ax2+2x,g(x)=lnx,
ax2+2x,g(x)=lnx,(1)如果函数y=f(x)在[1,+∞)上是单调增函数,求a的取值范围;
(2)是否存在实数a>0,使得方程
 =f′(x)-(2a+1)在区间
=f′(x)-(2a+1)在区间 内有且只有两个不相等的实数根?若存在,请求出a的取值范围;若不存在,请说明理由.
内有且只有两个不相等的实数根?若存在,请求出a的取值范围;若不存在,请说明理由. 解:(1)当a=0时,f(x)=2x在[1,+∞)上是单调增函数,符合题意;
当a>0时,y=f(x)的对称轴方程为 ,
,
由于y=f(x)在[1,+∞)上是单调增函数,
所以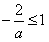 ,解得a≤-2或a>0,所以a>0;
,解得a≤-2或a>0,所以a>0;
当a<0时,不符合题意;
综上,a的取值范围是a≥0.
(2)把方程 整理为
整理为 ,
,
即为方程 ,
,
设 ,
,
原方程在区间 内有且只有两个不相等的实数根,即为函数H(x)在区间
内有且只有两个不相等的实数根,即为函数H(x)在区间 内有且只有两个零点,
内有且只有两个零点,
 ,
,
令H′(x)=0,因为a>0,解得x=1或 (舍),
(舍),
当x∈(0,1)时,H′(x)<0,H(x)是减函数;
当x∈(1,+∞)时,H′(x)>0,H(x)是增函数.
H(x)在 内有且只有两个不相等的零点,
内有且只有两个不相等的零点,
只需 。
。
当a>0时,y=f(x)的对称轴方程为
 ,
,由于y=f(x)在[1,+∞)上是单调增函数,
所以
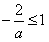 ,解得a≤-2或a>0,所以a>0;
,解得a≤-2或a>0,所以a>0;当a<0时,不符合题意;
综上,a的取值范围是a≥0.
(2)把方程
 整理为
整理为 ,
,即为方程
 ,
,设
 ,
,原方程在区间
 内有且只有两个不相等的实数根,即为函数H(x)在区间
内有且只有两个不相等的实数根,即为函数H(x)在区间 内有且只有两个零点,
内有且只有两个零点, ,
,令H′(x)=0,因为a>0,解得x=1或
 (舍),
(舍),当x∈(0,1)时,H′(x)<0,H(x)是减函数;
当x∈(1,+∞)时,H′(x)>0,H(x)是增函数.
H(x)在
 内有且只有两个不相等的零点,
内有且只有两个不相等的零点,只需
 。
。 
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |