题目内容
已知函数f(x)
|
(1)求a的值,并在直线坐标系中画出函数f(x)的大致图象;
(2)求函数f(t)-9的零点;
(3)设q(t)=f(t+1)-f(t)(t∈R),求函数q(t)的单调递增区间.
分析:(1)先由x=8>3,且点Q在函数图象上得:6=(8-5)2-a,解得a值,最后写出函数表达式画出图象即可.
(2)根据f (x )=9,得 3-x=9或(x-5)2-3=9,解此指数方程即得;
(3)先对t进行分类讨论:当t≤-1时,当-1<t≤0时,当0<t≤2时,当2<t≤3时,当3<t 时,分别讨论其单调性,最后综合上述,函数q (t ) 的单调递增区间是即可.
(2)根据f (x )=9,得 3-x=9或(x-5)2-3=9,解此指数方程即得;
(3)先对t进行分类讨论:当t≤-1时,当-1<t≤0时,当0<t≤2时,当2<t≤3时,当3<t 时,分别讨论其单调性,最后综合上述,函数q (t ) 的单调递增区间是即可.
解答:解: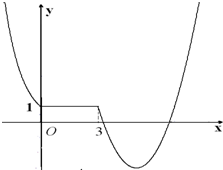 (1)由x=8>3,且点Q在函数图象上得:
(1)由x=8>3,且点Q在函数图象上得:
6=( 8-5 ) 2-a,解得a=3.
得f ( x )=
(2分)
图象如图所示.(2分)
(2)由f (x )=9,得 3-x=9或(x-5)2-3=9,
解得:x=-2,或x=5 ±2
(负舍去)
得 x=-2,或x=5 +2
.(2分)
(3)当t≤-1时,q (t )=f (t+1 )-f ( t )=3-t-1-3-t=-
(
)t,
此时,q (t )单调递增;
当-1<t≤0时,q (t )=f (t+1 )-f ( t )=1-3-t=1-(
)t,
此时,q (t )单调递增;
当0<t≤2时,q (t )=f (t+1 )-f ( t )=1-1=0,此时,q (t )是常数函数;
当2<t≤3时,q (t )=f (t+1 )-f ( t )=(t-4 )2-4,此时,q (t )单调递减;
当3<t 时,q (t )=f (t+1 )-f ( t )=(t-4 )2-3-(t-5 )2+3=2t-9,此时,q (t )单调递增.
综合上述,函数q (t ) 的单调递增区间是(-∞,0]和[3,+∞].(4分)
注:正确给出递增区间(2分),有说明(2分).
 (1)由x=8>3,且点Q在函数图象上得:
(1)由x=8>3,且点Q在函数图象上得:6=( 8-5 ) 2-a,解得a=3.
得f ( x )=
|
图象如图所示.(2分)
(2)由f (x )=9,得 3-x=9或(x-5)2-3=9,
解得:x=-2,或x=5 ±2
| 3 |
得 x=-2,或x=5 +2
| 3 |
(3)当t≤-1时,q (t )=f (t+1 )-f ( t )=3-t-1-3-t=-
| 2 |
| 3 |
| 1 |
| 3 |
此时,q (t )单调递增;
当-1<t≤0时,q (t )=f (t+1 )-f ( t )=1-3-t=1-(
| 1 |
| 3 |
此时,q (t )单调递增;
当0<t≤2时,q (t )=f (t+1 )-f ( t )=1-1=0,此时,q (t )是常数函数;
当2<t≤3时,q (t )=f (t+1 )-f ( t )=(t-4 )2-4,此时,q (t )单调递减;
当3<t 时,q (t )=f (t+1 )-f ( t )=(t-4 )2-3-(t-5 )2+3=2t-9,此时,q (t )单调递增.
综合上述,函数q (t ) 的单调递增区间是(-∞,0]和[3,+∞].(4分)
注:正确给出递增区间(2分),有说明(2分).
点评:本小题主要考查函数单调性的应用、函数的零点、函数的单调性及单调区间等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |