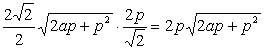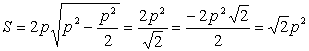题目内容
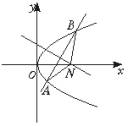
已知抛物线y2=2px(p>0).过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,|AB|≤2p.(Ⅰ)求a的取值范围;
(Ⅱ)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
答案:
解析:
解析:
| 解:(Ⅰ)设y=x-a,∴(x-a)2=2px
x2-2ax+a2-2px=0 x2-(2a+2p)x+a2=0 |AB|= ∴4ap+2p2≤p2,4ap≤-p2 又∵p>0,∴a≤- (Ⅱ)∵AB中点x=a+p y1+y2=x1+x2-2a y1+y2=2p ∴y=p ∴过N的直线l:y-p=-(x-a-p)+p=x-a-px=a+2p N到AB的距离为: ∴S= 当a有最大值时,S有最大值
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目