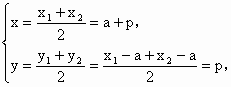已知抛物线y2＝2px且斜率为1的直线l与该抛物线交于不同的两点A.B.①若|AB|≤2p.求a的取值范围,②若线段AB的垂直平分线交AB于点Q.交x轴于点N.求直角三角形MNQ的面积．题目和参考答案——青夏教育精英家教网—

题目内容

已知抛物线y²＝2px(p＞0)，过动点M(a，0)且斜率为1的直线l与该抛物线交于不同的两点A、B，①若|AB|≤2p，求a的取值范围；②若线段AB的垂直平分线交AB于点Q，交x轴于点N，求直角三角形MNQ的面积．

答案：
解析：

　　解：①依题可得直线l的方程为y＝x－a，代入抛物线方程，整理得

　　x²－2(a＋p)x＋a²＝0，由韦达定理得x₁＋x₂＝2(a＋p)，x₁x₂＝a²．

　　依据弦长公式|AB|＝·|x₁－x₂|，可求得|AB|＝，∴0＜≤2p．

　　解得－＜a≤－，即为所求的取值范围．

　　②设Q(x，y)，由中点坐标公式得：

　　由两点间距离公式得|MQ|²＝2p²，又∵直线的斜率为1，

　　∴△MNQ为等腰直角三角形，

　　∴S_△MNQ＝|MQ|²＝p²．

练习册系列答案

复习直升机系列答案

相关题目

在直角坐标系xoy中，已知抛物线y²＝2px(p＞0)，过点(2p，0)作直线交抛物线于A(x₁，y₁)、B(x₂，y₂)两点，给出下列结论：(1)OA⊥OB(2)△AOB的最小面积是4p²(3)x₁x₂＝－4p²其中正确的结论是________．

（Ⅰ）求a的取值范围；

（Ⅱ）若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值.

如图所示，已知抛物线y²＝2px(p＞0)，过动点M(a，0)且斜率为1的直线l与该抛物线交于不同的两点A、B，且|AB|≤2p．

(1)求a的取值范围；

(2)若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值．

已知抛物线y²＝2px(p＞0)的焦点为F，准线为l．

(Ⅰ)求抛物线上任意一点Q到定点N(2p，0)的最近距离；

(Ⅱ)过点F作一直线与抛物线相交于A、B两点，并在准线l上任取一点M，当M不在x轴上时，证明：是一个定值，并求出这个值．

试题分类