题目内容
(1)在同一平面直角坐标系中,求下列方程所对应的图形经过伸缩变换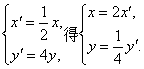 后的图形.
后的图形.①y2=2x;②y=3sin2x.
(2)将曲线C按伸缩变换公式![]() 变换后的曲线方程为x'2+y'2=1,则曲线C的方程为( )
变换后的曲线方程为x'2+y'2=1,则曲线C的方程为( )
A.![]()
B.![]()
C.4x2+9y2=36
D.4x2+9y2=1
解:(1)由伸缩变换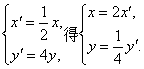 (*)
(*)
①将(*)代入y2=2x,得(![]() y')2=2·(2x').
y')2=2·(2x').
∴y'2=64x'.
∴经过伸缩变换后抛物线y2=2x变成了抛物线y'2=64x'.
②将(*)代入y=3sin2x,得![]() y'=3sin2·(2x'),?
y'=3sin2·(2x'),?
∴y'=12sin4x'.
∴经过伸缩变换后,曲线y=3sin2x变成了曲线y'=12sin4x'.?
(2)将![]() 代入方程x'2+y'2=1,得4x2+9y2=1.?
代入方程x'2+y'2=1,得4x2+9y2=1.?
故选D.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目



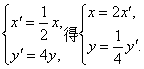 后的图形.
后的图形.