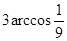题目内容
正四棱锥V—ABCD的五个顶点在同一个球面上，若其底面边长为4，侧棱长为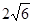
，
则AB两点的球面距为（ ）
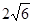，则AB两点的球面距为（ ）
A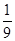． | B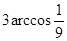． | C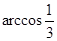． | D． |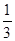
B
正四棱锥V—ABCD的高为h,则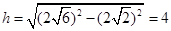
，设球半径为R,则
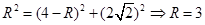；设AB所对的球心角为
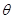。由余弦定理得：
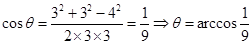。所以AB两点的球面距离是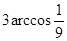
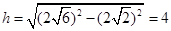，设球半径为R,则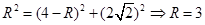；设AB所对的球心角为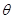。由余弦定理得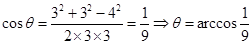：。所以AB两点的球面距离是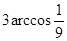
练习册系列答案
相关题目
题目内容
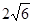，| A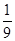． | B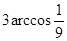． | C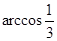． | D． |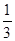
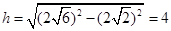，设球半径为R,则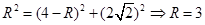；设AB所对的球心角为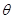。由余弦定理得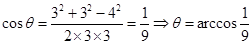：。所以AB两点的球面距离是
的球
的直径
垂直于平面
，垂足为
，
是平面
、
分别与球面交于点M，N，那么M、N两点间的球面距离是( )
是
所在平面外的一点，且
，若
内的射影落在
ABC外部，则
直线l , 则由点P和直线l确定的平面的个数是 
平面ABC，
，过A作SB的垂线，垂足为E，过E作SC的垂线，垂足为F，求证：⑴
；⑵
.
的两边
互相垂直，且
,则
边上的高
；现在把结论类比到空间：三棱锥
的三条侧棱
两两相互垂直，
平面
,且
,则点
到平面
中，
底面
，
，
，
是
的中点．
和平面
所成的角的大小；
平面
；