题目内容
已知z=x+yi(x,y∈R),且 2x+y+ilog2x-8=(1-log2y)i,则z=
- A.2+i
- B.1+2i
- C.2+i或1+2i
- D.无解
C
分析:由两个复数相等的条件把给出的等式转化为x,y的二元一次方程组,求解x,y即可.
解答:由 2x+y+ilog2x-8=(1-log2y)i,得:2x+y-8+ilog2x=(1-log2y)i
所以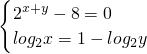 ,即
,即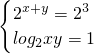 ,也就是
,也就是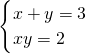 ,
,
解得: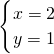 ,或
,或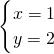 .
.
由z=x+yi,所以,z=2+i或1+2i.
故选C.
点评:本题考查了复数相等的充要条件,两个复数相等,当且仅当实部等于实部,虚部等于虚部,考查了方程组的解法,此题是基础题.
分析:由两个复数相等的条件把给出的等式转化为x,y的二元一次方程组,求解x,y即可.
解答:由 2x+y+ilog2x-8=(1-log2y)i,得:2x+y-8+ilog2x=(1-log2y)i
所以
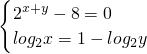 ,即
,即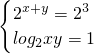 ,也就是
,也就是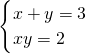 ,
,解得:
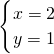 ,或
,或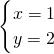 .
.由z=x+yi,所以,z=2+i或1+2i.
故选C.
点评:本题考查了复数相等的充要条件,两个复数相等,当且仅当实部等于实部,虚部等于虚部,考查了方程组的解法,此题是基础题.

练习册系列答案
相关题目