题目内容
17.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(1-x),求f(x)的解析式.分析 先利用奇函数的图象关于原点对称,利用奇函数的定义求出函数f(x)的解析式.
解答 解:由题意,当x=0时,f(x)=0
∵当x≥0时,f(x)=x(1-x),
∴当x<0时,-x>0,f(-x)=-x(x+1),
又∵函数y=f(x)是定义在R上的奇函数,
∴x<0时,f(x)=-f(-x)=x(x+1),
综上所述,f(x)=$\left\{\begin{array}{l}{x(1-x),x≥0}\\{x(1+x),x<0}\end{array}\right.$.
点评 本题考查了奇偶性的应用.若已知一个函数为奇函数,则应有其定义域关于原点对称,且对定义域内的一切x都有f(-x)=-f(x)成立.

练习册系列答案
相关题目
7.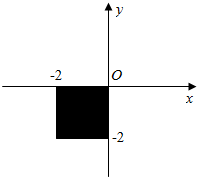 用描述法表示下图所示阴影部分的点(包括边界上的点)的坐标的集合是( )
用描述法表示下图所示阴影部分的点(包括边界上的点)的坐标的集合是( )
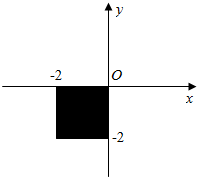 用描述法表示下图所示阴影部分的点(包括边界上的点)的坐标的集合是( )
用描述法表示下图所示阴影部分的点(包括边界上的点)的坐标的集合是( )| A. | {-2≤x≤0且-2≤y≤0} | B. | {(x,y)|-2≤x≤0且-2≤y≤0} | ||
| C. | {(x,y)|-2≤x≤0且-2≤y<0} | D. | {(x,y)|-2≤x≤0或-2≤y≤0} |
8.已知二次函数y=f(x)的图象开口向下,且f(3-x)=f(3+x),则下列结论中,错误的是( )
| A. | f(0)<f(7) | B. | f(6)<f(4) | C. | f(2)<f($\sqrt{15}$) | D. | f(3+$\sqrt{2}$)=f(3-$\sqrt{2}$) |
5.函数的图象与x=1的交点最多有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 以上都不对 |
 如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大,并求最大面积?
如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大,并求最大面积?