题目内容
.如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).(1)若二面角P-AB-Q的正切值为-3,试确定O在线段PQ的位置;(2)在(1)的前提下,以P,A,B,C,D,Q为顶点的几何体PABCDQ是否存在内切球?若存在,试确定其内切球心的具体位置;若不存在,请说明理由.
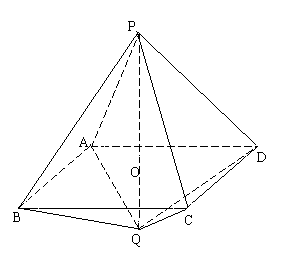 |
解:(1)取线段AB的中点为点E,则![]()
 设
设![]() ,
,![]() ,
,![]() ,
,![]()
故![]() ,
,![]()
由![]() ,
,
得:![]()
∵PO>OQ ∴![]()
故![]() 在线段PQ上的靠近Q点的三分点位置;
在线段PQ上的靠近Q点的三分点位置;
(2)几何体PABCDQ存在内切球,令球心为![]() ,
,
设线段CD的中点为点F,内切球的半径为![]() ,由对称性可知:平面四边形PEQF的内切圆的半径即为
,由对称性可知:平面四边形PEQF的内切圆的半径即为![]() ,故
,故![]()
所以![]() ,得
,得![]()
由三角形相似有:![]()
所以![]() 故其内切球心
故其内切球心![]() 在点P距离为
在点P距离为![]() 的位置上.
的位置上.
(注:也可用分割体积法求![]() )
)

练习册系列答案
相关题目
 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.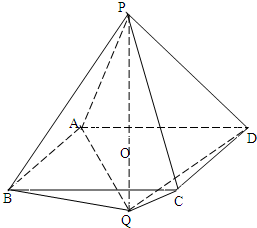 如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).
如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ). 如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).
如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).