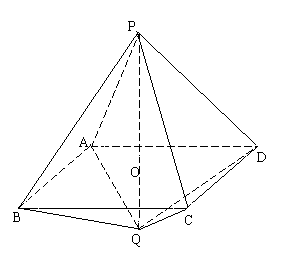题目内容
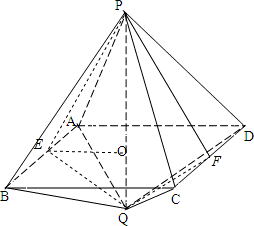
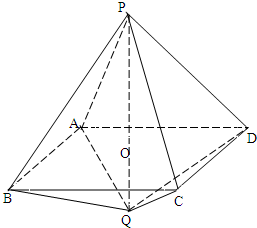 如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).
如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).
(1)若二面角P-AB-Q的正切值为-3,试确定O在线段PQ的位置;
(2)在(1)的前提下,以P,A,B,C,D,Q为顶点的几何体PABCDQ是否存在内切球?若存在,试确定其内切球心的具体位置;若不存在,请说明理由.
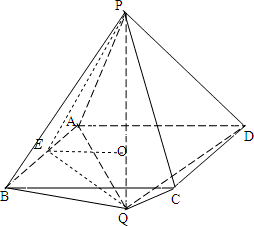 解:(1)取线段AB的中点为点E,
解:(1)取线段AB的中点为点E,连接PE,OE,QE.由于四边形ABCD是正方形,O为其中心,所以OE⊥AB,
又PO⊥面ABCD AB?面ABCD,所以PO⊥AB,
而 OE∩AB=O,所以AB⊥面PEO,PE?面PEO,所以AB⊥PE,
同理可以证出AB⊥QE,∴∠PEQ为二面角P-AB-Q的平面角,tan∠PEQ=-3.
设∠PEQ=α,∠QEO=β,OP=x,则OQ=3-x.且OE=1
在RT△PEO中,tanα=
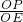 =x,
=x,同理在RT△QEO中,tanβ=
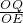 =3-x
=3-x由tan∠PEQ=tan(α+β)=
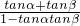 =
=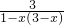 =-3,
=-3,得:x2-3x+2=0
∵PO>OQ∴OP=x=2
故O在线段PQ上的靠近Q点的三分点位置;
(2)几何体PABCDQ存在内切球,令球心为O′,
若设线段CD的中点为点F,内切球的半径为r,由对称性可知:平面四边形PEQF的内切圆的圆心为O′,半径即为r,
故SPEQF=
 EF•PQ=
EF•PQ= r(2PE+2QE),而PE=
r(2PE+2QE),而PE=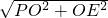 =
= ,QE=
,QE=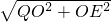 =
= .
.所以
 ×2×3=
×2×3= r(2
r(2 +2
+2 ),得r=
),得r= -
- .
.由三角形相似有:
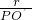 =sin∠EPO=
=sin∠EPO=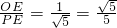
所以PO′=
 r=5-
r=5- .故其内切球心O′在点P距离为5-
.故其内切球心O′在点P距离为5- 的位置上.
的位置上.(注:也可用分割体积法求r)
分析:(1)取线段AB的中点为点E,连接PE,OE,可以证明,∠PEQ为二面角P-AB-Q的平面角,且tan∠PEQ=-3.将∠PEQ 看作∠PEQ与∠QEO之和.设OP=x,利用两角和的正切公式,建立关于x的方程并解出即可.
(2)若设线段CD的中点为点F,由对称性可知:平面四边形PEQF的内切圆的圆心为O′,半径即为r,利用分割面积法可以求出r的值,O′在PQ上.在四边形PEQF中利用平面几何知识确定出内切球心的具体位置.
点评:本题考查了二面角的定义,度量,方程思想.还考查了组合体的几何性质,面积(体积)分割的思想.本题中的几何体实际上是由两个同底不等高的正四棱锥组合而成.

练习册系列答案
相关题目
 如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.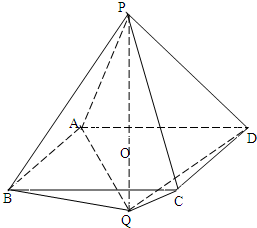 如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).
如图:长为3的线段PQ与边长为2的正方形ABCD垂直相交于其中心O(PO>OQ).