题目内容
已知函数
(1)若 的定义域是
的定义域是 ,求实数
,求实数 的取值范围及
的取值范围及 的值域;
的值域;
(2)若 的值域是
的值域是 ,求实数
,求实数 的取值范围及
的取值范围及 的定义域
的定义域
(Ⅰ) ;
; (Ⅱ)
(Ⅱ) ,
,
解析试题分析:在这里,第一问和第二问,同学们一般搞不清,感觉两种条件下列式是一样的.但其实第一问中要求真数部分要大于0恒成立.但第二问却是,要保证值域为R,定义域必须保证是 的子集.
的子集.
试题解析:(1)因为 定义域为R,所以
定义域为R,所以 对一切
对一切 成立,
成立,
由此得 解得
解得 3分
3分
又因为
所以
 ,
,
所以实数 的取值范围是
的取值范围是
 的值域是
的值域是 6分
6分
(2)因为 的值域是R,所以
的值域是R,所以 的值域
的值域
当 时,
时, 的值域为R
的值域为R ;
;
当 时,
时, 的值域
的值域 等价于
等价于
解得
所以实数 的取值范围是
的取值范围是 9分
9分
当 由
由 得
得 ,
, 定义域为
定义域为 ; 10分
; 10分
当 时,由
时,由 解得
解得 或
或
所以 得定义域是
得定义域是 12分
12分
考点:对数函数的定义域和值域.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度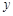 (克/升)随着时间
(克/升)随着时间 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为 ,其中
,其中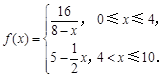 若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.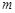 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求 .
. 时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围. 中,已知椭圆
中,已知椭圆 :
: 的离心率
的离心率 ,且椭圆C上一点
,且椭圆C上一点 到点Q
到点Q 的距离最大值为4,过点
的距离最大值为4,过点 的直线交椭圆
的直线交椭圆
 (O为坐标原点),当
(O为坐标原点),当 时,求实数
时,求实数 的取值范围.
的取值范围. (a>0,a≠1)
(a>0,a≠1) 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围. 的解集为M.
的解集为M. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
. 的值;
的值; 在
在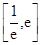 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(3)令
为自然对数的底数);(3)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 (其中
(其中 ),
), 的中点为
的中点为 ,求证:
,求证: 处的导数
处的导数
 、圆心角为
、圆心角为 的扇形的弧上任取一点
的扇形的弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在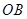 上,设矩形
上,设矩形 ,
,
 ,将
,将 的函数关系式;
的函数关系式; ,将
,将 的函数关系式;
的函数关系式;