题目内容
11.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足a+b=2$\sqrt{3}$,ab=2,2cos(A+B)=1.(1)求角C;
(2)求c的长;
(3)求△ABC的面积.
分析 (1)利用2cos(A+B)=1,求角C;
(2)利用余弦定理求c的长;
(3)利用△ABC的面积S=$\frac{1}{2}$absinC,求△ABC的面积.
解答 解:(1)∵2cos(A+B)=1,
∴cosC=-$\frac{1}{2}$,
∴C=120°;
(2)∵a+b=2$\sqrt{3}$,ab=2,
∴a2+b2=8,
∴c2=a2+b2-2accosC=8-2×2×(-$\frac{1}{2}$)=10,
∴c=$\sqrt{10}$;
(3)△ABC的面积S=$\frac{1}{2}$absinC=$\frac{1}{2}×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查余弦定理,考查三角形面积的就算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.猜测(1-$\frac{4}{1}$)(1-$\frac{4}{9}$)…[1一$\frac{4}{(2n-1)^{2}}$]对n∈N且n≥1成立的-个表达式为 ( )
| A. | -$\frac{n+2}{n}$ | B. | $\frac{2n+1}{2n-1}$ | C. | $-\frac{2n+1}{2n-1}$ | D. | -$\frac{n+1}{n-1}$ |
3.已知直线l与曲线f(x)=x2-3x+2+2lnx相切,则直线l倾斜角的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
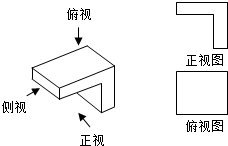 在如图中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确的吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求)
在如图中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确的吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求)