题目内容
在△ABC中AB=c,AC=b,D为线段BC上一点,且∠BAD=α,∠CAD=β,线段AD=l.
(1)求证:
+
=
(2)若AB=4
,AC=4,∠BAD=30°,∠CAD=45°,试求线段AD的长.
(1)求证:
| sinα |
| b |
| sinβ |
| c |
| sin(α+β) |
| l |
(2)若AB=4
| 2 |
分析:(1)在△ABC中,S△ABC=S△ABD+S△BCD,再同除
bcl即得结论;
(2)由(1)代入数据,可求线段AD的长.
| 1 |
| 2 |
(2)由(1)代入数据,可求线段AD的长.
解答:(1)证明:在△ABC中,S△ABC=S△ABD+S△BCD,得
bcsin(α+β)=
blsinβ+
clsinα,
同除
bcl即得
+
=
;
(2)解:由(1)代入数据得
+
=
,解得l=
+
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
同除
| 1 |
| 2 |
| sinα |
| b |
| sinβ |
| c |
| sin(α+β) |
| l |
(2)解:由(1)代入数据得
| sin30° |
| 4 |
| sin45° | ||
4
|
| sin(30°+45°) |
| l |
| 6 |
| 2 |
点评:本题考查三角形面积公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
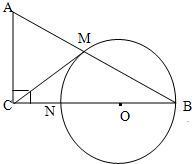 如图,在△ABC中,∠C=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.
如图,在△ABC中,∠C=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.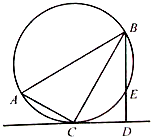 (2013•重庆)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为
(2013•重庆)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为