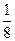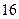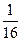题目内容
对函数f(x),若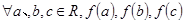 为某一个三角形的边长,则称
为某一个三角形的边长,则称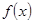 为“
为“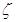 三角函数”,已知函数
三角函数”,已知函数 为“
为“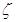 三角函数”,则实数m的取值范围是 ( )
三角函数”,则实数m的取值范围是 ( )
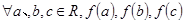 为某一个三角形的边长,则称
为某一个三角形的边长,则称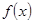 为“
为“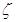 三角函数”,已知函数
三角函数”,已知函数 为“
为“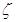 三角函数”,则实数m的取值范围是 ( )
三角函数”,则实数m的取值范围是 ( )A.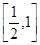 | B.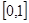 | C.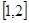 | D.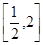 |
D
试题分析:由三角形的性质可知:构成三角形三边的长必须且只需满足:任意两边之和大于第三边;则由已知函数

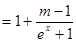 ,由题意,f(x)>0恒成立,即
,由题意,f(x)>0恒成立,即 ,①若0<m≤1,则f(x)为增函数,当x取正无穷时,f(x)取最大值1,当x取负无穷时,f(x)取最小值m,即f(x)值域为(m,1),又知三角形两边之和大于第三边,故应有m+m≥1,解得
,①若0<m≤1,则f(x)为增函数,当x取正无穷时,f(x)取最大值1,当x取负无穷时,f(x)取最小值m,即f(x)值域为(m,1),又知三角形两边之和大于第三边,故应有m+m≥1,解得 ≤m≤1;②若m>1,则f(x)为减函数,当x取正无穷时,f(x)取最小值1,当x取负无穷时,f(x)取最大值m;即f(x)值域为(1,m),同理,有1+1≥m,得1<m≤2;综上,得t的取值范围为[
≤m≤1;②若m>1,则f(x)为减函数,当x取正无穷时,f(x)取最小值1,当x取负无穷时,f(x)取最大值m;即f(x)值域为(1,m),同理,有1+1≥m,得1<m≤2;综上,得t的取值范围为[ ,2];故选D.
,2];故选D.
练习册系列答案
相关题目
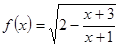 的定义域为
的定义域为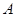 ,
,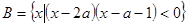 .
.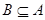 ,求实数
,求实数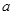 的取值范围.
的取值范围. 的定义域是( )
的定义域是( )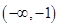
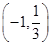
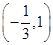
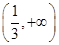
 的导函数为
的导函数为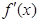 ,当
,当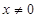 时,
时,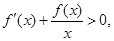 若
若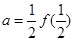 ,
,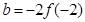 ,
,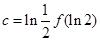 ,则
,则 的大小关系是 .
的大小关系是 .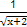 的定义域是( )
的定义域是( )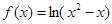 的定义域为( )
的定义域为( )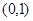
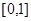
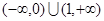
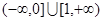
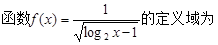 ( )
( )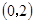
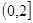

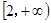
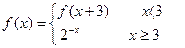 则
则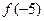 的值为( )
的值为( )