题目内容
【题目】已知向量![]() 垂直于向量
垂直于向量![]() ,向量
,向量![]() 垂直于向量
垂直于向量![]() .
.
(1)求向量![]() 与
与![]() 的夹角;
的夹角;
(2)设![]() ,且向量
,且向量![]() 满足
满足![]() ,求
,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,随机选取一个向量![]() ,求
,求![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据向量的垂直,转化出方程组,求解方程组即可;
(2)将向量赋予坐标,求得向量对应点的轨迹方程,将问题转化为圆外一点,到圆上一点的距离的最值问题,即可求解;
(3)根据余弦定理,解得![]() ,以及
,以及![]() 的临界状态时,对应的圆心角的大小,利用几何概型的概率计算公式,即可求解.
的临界状态时,对应的圆心角的大小,利用几何概型的概率计算公式,即可求解.
(1)因为![]()
故可得![]() ,
,![]()
解得![]() ①
①
![]() ②
②
由①-②可得
![]() ,解得
,解得![]() ,
,
将其代入①可得![]() ,即
,即![]()
将其代入②可得![]()
解得![]() ,又向量夹角的范围为
,又向量夹角的范围为![]() ,
,
故向量![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(2)不妨设![]() ,
,![]()
由![]()
可得![]() .
.
不妨设![]() 的起始点为坐标原点,终点为C.
的起始点为坐标原点,终点为C.
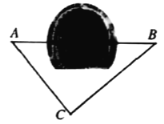
因此,点C落在以![]() )为圆心,1为半径的圆上(如图).
)为圆心,1为半径的圆上(如图).

因为![]() ,即
,即![]()
由圆的特点可知![]() 的最小值为
的最小值为![]() ,
,
即:![]() .
.
(3)当![]() 时,因为
时,因为![]() ,
,![]() ,满足勾股定理,
,满足勾股定理,
故容易得![]() .
.
当![]() 时,假设此时
时,假设此时![]() 点落在如图所示的F点处.如图所示.
点落在如图所示的F点处.如图所示.
因为![]() ,由余弦定理容易得
,由余弦定理容易得
![]() ,故
,故![]() .
.

所以,本题化为,在半圆上任取一点C,点C落在弧CF上的概率.
由几何概型的概率计算可知:
![]() 的概率即为圆心角
的概率即为圆心角![]() 的弧度除以
的弧度除以![]() ,
,
即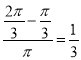 .
.

练习册系列答案
相关题目