题目内容
我们把形如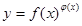 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得 ,两边对
,两边对 求导数,得
求导数,得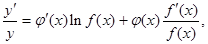 于是
于是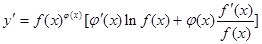 ,运用此方法可以求得函数
,运用此方法可以求得函数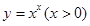 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________
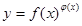 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得 ,两边对
,两边对 求导数,得
求导数,得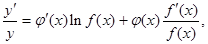 于是
于是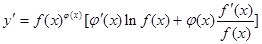 ,运用此方法可以求得函数
,运用此方法可以求得函数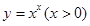 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________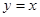
解:仿照题目给定的方法,f(x)=x,g(x)=x
所以f′(x)=1,g′(x)=1
所以,y′=(1×lnx+x•1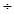 x )xx,
x )xx,
∴y′| x="1" =(1×lnx+x•1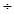 x )xx| x="1" =1,
x )xx| x="1" =1,
即:函数y="x" x (x>0)在(1,1)处的切线的斜率为1,
故切线方程为:y-1=x-1,即y=x
故答案为:y=x.
所以f′(x)=1,g′(x)=1
所以,y′=(1×lnx+x•1
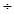 x )xx,
x )xx,∴y′| x="1" =(1×lnx+x•1
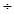 x )xx| x="1" =1,
x )xx| x="1" =1,即:函数y="x" x (x>0)在(1,1)处的切线的斜率为1,
故切线方程为:y-1=x-1,即y=x
故答案为:y=x.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
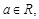 函数
函数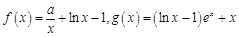
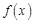 在
在 上的单调性;
上的单调性;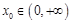 ,使曲线
,使曲线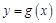 在点
在点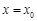 处的切线与
处的切线与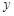 轴垂直?若存在,求出
轴垂直?若存在,求出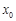 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 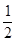 x
x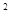 -ax+(a-1)
-ax+(a-1)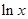 ,
,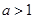 。
。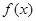 的单调性;
的单调性; 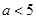 ,则对任意x
,则对任意x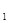 ,x
,x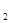
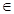
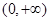 ,x
,x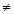 x
x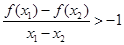 。
。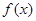 是定义在
是定义在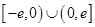 上的奇函数,当
上的奇函数,当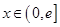 时,
时, 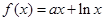 (其中e是自然界对数的底,
(其中e是自然界对数的底,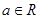 )
)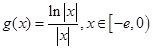 ,求证:当
,求证:当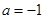 时,
时,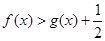 ;
;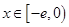 时,
时,
 ,其中
,其中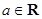 .
.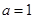 时,求曲线
时,求曲线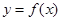 在原点处的切线方程;
在原点处的切线方程;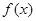 的单调区间.
的单调区间.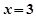 是函数
是函数 的一个极值点。
的一个极值点。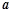 的值;
的值;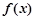 的单调区间;
的单调区间;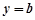 与函数
与函数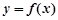 的图象有3个交点,求
的图象有3个交点,求 的取值范围。
的取值范围。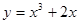 相切的直线方程为_______ __ ;
相切的直线方程为_______ __ ; 与
与 围成的区域面积为
围成的区域面积为 



