题目内容
(本小题满分12分) 如图,已知正三棱柱ABC-A1B1C1的各条棱长均为2,M是BC的中点.
(Ⅰ)求证:A1C∥面AB1M;
(Ⅱ)在棱CC1上找一点N,使MN⊥AB1;
(Ⅲ)在(Ⅱ)的条件下,求二面角M-AB1-N的大小.
(Ⅰ)证明:连结A1B,交AB1于P,则PM//A1C,又PMÌ面AB1M,A1CË面AB1M,
∴A1C∥面AB1M. 4分
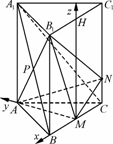 (Ⅱ)解:取B1C1中点H,连接MH,在正三棱柱ABC-A1B1C1中,
(Ⅱ)解:取B1C1中点H,连接MH,在正三棱柱ABC-A1B1C1中,![]() 、
、![]() 、
、![]() 两两垂直,故分别以
两两垂直,故分别以![]() 、
、![]() 、
、![]() 为x、y、z轴,建立如图空间坐标系.设
为x、y、z轴,建立如图空间坐标系.设![]() (
(![]() ),则
),则![]() ,
,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
由![]() ,有
,有![]() ,解得
,解得![]() ,故在棱CC1上的点N满足
,故在棱CC1上的点N满足![]() ,使MN⊥AB1. 8分
,使MN⊥AB1. 8分
(Ⅲ)解:由(Ⅱ),![]() ,
,![]() ,则
,则![]() ,
,![]() ,又
,又![]() ,则面AB1M一个法向量
,则面AB1M一个法向量![]() .
.
设面AB1N的一个法向量![]() ,
,![]() ,
,![]() ,
,
由![]() 即
即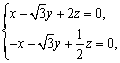 取
取![]() , 10分
, 10分
则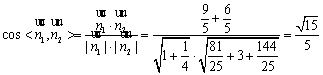 ,
,
故二面角M-AB1-N的大小为![]() . 12分
. 12分

练习册系列答案
相关题目