题目内容
已知数列的通项公式an=2n-37,则Sn取最小值时n=
18
18
,此时Sn=-324
-324
.分析:由an=2n-37,知{an}是首项为-35,公差为2的等差数列,故Sn=-35n+
× 2=n2-36n=(n-18)2-324,由此能得到当n=18时,Sn取最小值-324.
| n(n-1) |
| 2 |
解答:解:∵an=2n-37,
∴a1=2-37=-35,
a2=4-37=-33,
d=a2-a1=-33+35=2,
∴{an}是首项为-35,公差为2的等差数列,
∴Sn=-35n+
× 2
=n2-36n
=(n-18)2-324,
∴当n=18时,Sn取最小值S18=-324.
故答案为:18,-324.
∴a1=2-37=-35,
a2=4-37=-33,
d=a2-a1=-33+35=2,
∴{an}是首项为-35,公差为2的等差数列,
∴Sn=-35n+
| n(n-1) |
| 2 |
=n2-36n
=(n-18)2-324,
∴当n=18时,Sn取最小值S18=-324.
故答案为:18,-324.
点评:本题考查等差数列的前n项和的性质和应用,是基础题.解题时要认真审题,仔细解答,注意配方法的合理运用.

练习册系列答案
相关题目
已知数列的通项公式an=
(n∈N*),则数列{an}的前30项中最大值和最小值分别是( )
n-
| ||
n-
|
| A、a10,a9 |
| B、a10,a30 |
| C、a1,a30 |
| D、a1,a9 |
已知数列 的通项公式
的通项公式 ,设其前n项和为
,设其前n项和为 ,则使
,则使 成立的自然
成立的自然
数 有 ( )
有 ( )
| A.最大值15 | B.最小值15 | C.最大值16 | D.最小值16 |
 的通项公式为
的通项公式为 ,设其前
,设其前 项和为
项和为 ,则使
,则使 成立的最小自然数
成立的最小自然数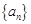 的通项公式为
的通项公式为 ,则数列
,则数列 成等比数列是数列
成等比数列是数列 的通项公式为
的通项公式为 的( ▲ )
的( ▲ )