题目内容
已知数列的通项公式an=
(n∈N*),则数列{an}的前30项中最大值和最小值分别是( )
n-
| ||
n-
|
| A、a10,a9 |
| B、a10,a30 |
| C、a1,a30 |
| D、a1,a9 |
分析:将数列的通项看成关于n的函数,将通项分离常数,利用反比例函数的单调性判断出数列的单调性,根据数列自变量的特殊性,求出数列的最大值及最小值.
解答:解:an=
=1+
当n≥10时,an=
=1+
>1,n-
为正值且随n减小而减小,则an越大;
数列{an}的前30项中最大值是a10,
当n≤9时,an=
=1+
<1,n-
为负值且随n减小而减小,则an越大;
数列{an}的前30项中最小值是a9,
∴数列{an}的前30项中最大值和最小值分别是a10,a9;
故选A.
n-
| ||
n-
|
| ||||
n-
|
当n≥10时,an=
n-
| ||
n-
|
| ||||
n-
|
| 98 |
数列{an}的前30项中最大值是a10,
当n≤9时,an=
n-
| ||
n-
|
| ||||
n-
|
| 98 |
数列{an}的前30项中最小值是a9,
∴数列{an}的前30项中最大值和最小值分别是a10,a9;
故选A.
点评:解决数列问题时,常将数列看成关于项数n的函数,处理函数的方法在数列中都能使用.注意数列是特殊的函数:自变量是正整数.

练习册系列答案
相关题目
已知数列 的通项公式
的通项公式 ,设其前n项和为
,设其前n项和为 ,则使
,则使 成立的自然
成立的自然
数 有 ( )
有 ( )
| A.最大值15 | B.最小值15 | C.最大值16 | D.最小值16 |
 的通项公式为
的通项公式为 ,设其前
,设其前 项和为
项和为 ,则使
,则使 成立的最小自然数
成立的最小自然数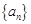 的通项公式为
的通项公式为 ,则数列
,则数列 成等比数列是数列
成等比数列是数列 的通项公式为
的通项公式为 的( ▲ )
的( ▲ )