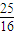题目内容
定长为10的线段AB的两端点都在抛物线y2=8x上,则AB中点M的横坐标的最小值为( )
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
分析:xM=
(xA+xB)=
(xA+
+xB+
) -
=
(|FA|+|FB|)=
,由|FA|+|FB|≥|AB|=10,知xM≥
×10-2=3.
| 1 |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
解答:解:xM=
(xA+xB)
=
(xA+
+xB+
) -
=
(|FA|+|FB|)=
,
∵|FA|+|FB|≥|AB|=10,
∴xM≥
×10-2=3,
当A,F,B三点共线时,取得最小值.
故选A.
| 1 |
| 2 |
=
| 1 |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
=
| 1 |
| 2 |
| p |
| 2 |
∵|FA|+|FB|≥|AB|=10,
∴xM≥
| 1 |
| 2 |
当A,F,B三点共线时,取得最小值.
故选A.
点评:本题考查抛物线的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目