题目内容
若奇函数f(x)在定义域(-1,1)上是减函数
(1)求满足f(1-a)+f(1-a2)<0的集合M
(2)对(1)中的a,求函数F(x)=loga[1-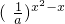 ]的定义域.
]的定义域.
解:(1)∵f(x)是奇函数,又f(1-a)+f(1-a2)<0,
∴f(1-a)<-f(1-a2)=f(a2-1)
又∵f(x)是减函数,
∴1-a>a2-1
再由x∈(-1,1)得-1<a2-1<1-a<1
即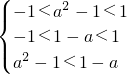 即
即
解得M={a|0<a<1}
(2)为使F(x)=loga[1-( )x2-x]有意义,
)x2-x]有意义,
则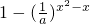 >0
>0
即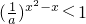
∵0<a<1,∴ ,u=
,u=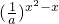 是增函数
是增函数
∴x2-x<0,解得0<x<1,
∴F(x)的定义域为{x|0<x<1}
分析:(1)由f(x)是奇函数,且f(1-a)+f(1-a2)<0,可得f(1-a)<-f(1-a2)=f(a2-1),结合f(x)在x∈(-1,1)是减函数得-1<a2-1<1-a<1,解不等式可求M
(2)由题意可得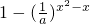 >0,结合0<a<1,可知,u=
>0,结合0<a<1,可知,u=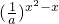 是增函数可得x2-x<0,可求
是增函数可得x2-x<0,可求
点评:本题主要考查了利用函数的奇偶性及函数的单调性解不等式,对数函数定义域的求解及知识函数单调性的应用,属于函数知识的综合应用.
∴f(1-a)<-f(1-a2)=f(a2-1)
又∵f(x)是减函数,
∴1-a>a2-1
再由x∈(-1,1)得-1<a2-1<1-a<1
即
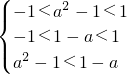 即
即
解得M={a|0<a<1}
(2)为使F(x)=loga[1-(
 )x2-x]有意义,
)x2-x]有意义,则
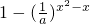 >0
>0即
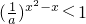
∵0<a<1,∴
 ,u=
,u=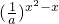 是增函数
是增函数∴x2-x<0,解得0<x<1,
∴F(x)的定义域为{x|0<x<1}
分析:(1)由f(x)是奇函数,且f(1-a)+f(1-a2)<0,可得f(1-a)<-f(1-a2)=f(a2-1),结合f(x)在x∈(-1,1)是减函数得-1<a2-1<1-a<1,解不等式可求M
(2)由题意可得
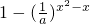 >0,结合0<a<1,可知,u=
>0,结合0<a<1,可知,u=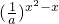 是增函数可得x2-x<0,可求
是增函数可得x2-x<0,可求点评:本题主要考查了利用函数的奇偶性及函数的单调性解不等式,对数函数定义域的求解及知识函数单调性的应用,属于函数知识的综合应用.

练习册系列答案
相关题目
 ]的定义域.
]的定义域.