题目内容
若奇函数f(x)在定义域(-1,1)上是减函数
(1)求满足f(1-a)+f(1-a2)<0的集合M
(2)对(1)中的a,求函数F(x)=loga[1-(
)x2-x]的定义域.
(1)求满足f(1-a)+f(1-a2)<0的集合M
(2)对(1)中的a,求函数F(x)=loga[1-(
| 1 |
| a |
(1)∵f(x)是奇函数,又f(1-a)+f(1-a2)<0,
∴f(1-a)<-f(1-a2)=f(a2-1)
又∵f(x)是减函数,
∴1-a>a2-1
再由x∈(-1,1)得-1<a2-1<1-a<1
即
即
解得M={a|0<a<1}
(2)为使F(x)=loga[1-(
)x2-x]有意义,
则1-(
)x2-x>0
即(
)x2-x<1
∵0<a<1,∴
>1,u=(
)x2-x是增函数
∴x2-x<0,解得0<x<1,
∴F(x)的定义域为{x|0<x<1}
∴f(1-a)<-f(1-a2)=f(a2-1)
又∵f(x)是减函数,
∴1-a>a2-1
再由x∈(-1,1)得-1<a2-1<1-a<1
即
|
|
解得M={a|0<a<1}
(2)为使F(x)=loga[1-(
| 1 |
| a |
则1-(
| 1 |
| a |
即(
| 1 |
| a |
∵0<a<1,∴
| 1 |
| a |
| 1 |
| a |
∴x2-x<0,解得0<x<1,
∴F(x)的定义域为{x|0<x<1}

练习册系列答案
相关题目
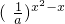 ]的定义域.
]的定义域. ]的定义域.
]的定义域.