题目内容
若奇函数f(x)在定义域(-1,1)上递减,且f(1-a)+f(1-a2)>0,则α的取值范围是
1<a<
| 2 |
1<a<
.| 2 |
分析:利用函数的单调性、奇偶性可去掉不等式f(1-a)+f(1-a2)>0中的符号“f”,再考虑函数的定义域可得不等式组,解出即可.
解答:解:因为f(x)为奇函数,所以f(1-a)+f(1-a2)>0可化为f(1-a)>-f(1-a2)=f(a2-1),
又f(x)在定义域(-1,1)上递减,
所以有
,解得1<a<
.
所以a的取值范围为:1<a<
.
故答案为:1<a<
.
又f(x)在定义域(-1,1)上递减,
所以有
|
| 2 |
所以a的取值范围为:1<a<
| 2 |
故答案为:1<a<
| 2 |
点评:本题考查函数的奇偶性、单调性的综合应用,考查抽象不等式的求解,考查学生的转化能力.

练习册系列答案
相关题目
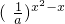 ]的定义域.
]的定义域. ]的定义域.
]的定义域.