题目内容
9.平面内有n(n∈N*,n≥2)条直线,其中任何两条不平行,任何三条不过同一点,证明交点的个数f(n)=$\frac{n(n-1)}{2}$.分析 利用数学归纳法的证明步骤,即可证明结论.
解答 证明:(1)当n=2时,两条直线的交点只有一个,又f(2)=$\frac{1}{2}$×2×(2-1)=1,
∴当n=2时,命题成立.
(2)假设n=k∈N*,且(k>2)时,命题成立,即平面内满足题设的任何k条直线交点个数f(k)=$\frac{1}{2}$k(k-1),
那么,当n=k+1时,任取一条直线l,除l以外其他k条直线交点个数为f(k)=$\frac{1}{2}$k(k-1),l与其他k条直线交点个数为k,从而k+1条直线共有f(k)+k个交点,
即f(k+1)=f(k)+k=$\frac{1}{2}$k(k-1)+k=$\frac{1}{2}$k(k-1+2)=$\frac{1}{2}$k(k+1)=$\frac{1}{2}$(k+1)[(k+1)-1],
这表明,当n=k+1时,命题成立.
由(1)、(2)可知,对n∈N*(n≥2)命题都成立.
点评 本题考查数学归纳法,考查学生分析解决问题的能力,证明n=k+1时结论成立是关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
19.已知i是虚数单位,则$(\frac{1-i}{1+i})^{2}$=( )
| A. | 1 | B. | i | C. | -i | D. | -1 |
4.如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )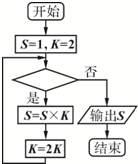

| A. | k<32? | B. | k<63? | C. | k<64? | D. | k<70? |
 在如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.