题目内容
已知抛物线C的一个焦点为 ,其准线方程为
,其准线方程为
(1)写出抛物线C的方程;
(2)过F点的直线与曲线C交于A、B两点,O点为坐标原点,求△AOB重心G的轨迹方程.
【答案】分析:(1)根据抛物线C的一个焦点为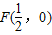 ,其准线方程为
,其准线方程为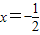 ,可得抛物线C的方程为y2=2x;
,可得抛物线C的方程为y2=2x;
(2)①当直线l不垂直于x轴时,设方程为y=k(x- ),代入y2=2x,得k2x2-x(k2+2)+
),代入y2=2x,得k2x2-x(k2+2)+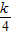 =0.设点A、B的坐标分别为(x1,y1)、(x2,y2),根据韦达定理,及三角形的重心坐标公式,即可求出△AOB重心G的轨迹方程;②当l垂直于x轴时,A、B的坐标分别为(
=0.设点A、B的坐标分别为(x1,y1)、(x2,y2),根据韦达定理,及三角形的重心坐标公式,即可求出△AOB重心G的轨迹方程;②当l垂直于x轴时,A、B的坐标分别为( ,1)和(
,1)和( ,-1),△AOB的重心G(
,-1),△AOB的重心G( ,0),也适合y2=
,0),也适合y2= x-
x- ,故可得轨迹C的方程.
,故可得轨迹C的方程.
解答:解:(1)∵抛物线C的一个焦点为 ,其准线方程为
,其准线方程为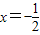
∴抛物线C的方程为y2=2x;
(2)抛物线的焦点坐标为( ,0),
,0),
①当直线l不垂直于x轴时,设方程为y=k(x- ),代入y2=2x,
),代入y2=2x,
得k2x2-x(k2+2)+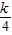 =0.
=0.
设l方程与抛物线相交于两点,∴k≠0.设点A、B的坐标分别为(x1,y1)、(x2,y2),
根据韦达定理,有x1+x2=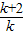 ,从而y1+y2=k(x1+x2-1)=
,从而y1+y2=k(x1+x2-1)= .
.
设△AOB的重心为G(x,y),则x=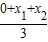 =
=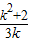 ,y=
,y=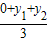 =
=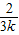 ,
,
∴y2= x-
x- .
.
②当l垂直于x轴时,A、B的坐标分别为( ,1)和(
,1)和( ,-1),△AOB的重心G(
,-1),△AOB的重心G( ,0),也适合y2=
,0),也适合y2= x-
x- ,
,
因此所求轨迹C的方程为y2= x-
x- .
.
点评:本题重点考查抛物线的方程,考查抛物线的性质,考查韦达定理的运用,解题的关键是直线与抛物线联立,利用韦达定理解决.
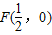 ,其准线方程为
,其准线方程为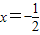 ,可得抛物线C的方程为y2=2x;
,可得抛物线C的方程为y2=2x;(2)①当直线l不垂直于x轴时,设方程为y=k(x-
 ),代入y2=2x,得k2x2-x(k2+2)+
),代入y2=2x,得k2x2-x(k2+2)+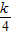 =0.设点A、B的坐标分别为(x1,y1)、(x2,y2),根据韦达定理,及三角形的重心坐标公式,即可求出△AOB重心G的轨迹方程;②当l垂直于x轴时,A、B的坐标分别为(
=0.设点A、B的坐标分别为(x1,y1)、(x2,y2),根据韦达定理,及三角形的重心坐标公式,即可求出△AOB重心G的轨迹方程;②当l垂直于x轴时,A、B的坐标分别为( ,1)和(
,1)和( ,-1),△AOB的重心G(
,-1),△AOB的重心G( ,0),也适合y2=
,0),也适合y2= x-
x- ,故可得轨迹C的方程.
,故可得轨迹C的方程.解答:解:(1)∵抛物线C的一个焦点为
 ,其准线方程为
,其准线方程为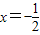
∴抛物线C的方程为y2=2x;
(2)抛物线的焦点坐标为(
 ,0),
,0),①当直线l不垂直于x轴时,设方程为y=k(x-
 ),代入y2=2x,
),代入y2=2x,得k2x2-x(k2+2)+
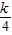 =0.
=0.设l方程与抛物线相交于两点,∴k≠0.设点A、B的坐标分别为(x1,y1)、(x2,y2),
根据韦达定理,有x1+x2=
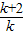 ,从而y1+y2=k(x1+x2-1)=
,从而y1+y2=k(x1+x2-1)= .
.设△AOB的重心为G(x,y),则x=
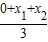 =
=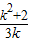 ,y=
,y=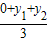 =
=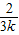 ,
,∴y2=
 x-
x- .
.②当l垂直于x轴时,A、B的坐标分别为(
 ,1)和(
,1)和( ,-1),△AOB的重心G(
,-1),△AOB的重心G( ,0),也适合y2=
,0),也适合y2= x-
x- ,
,因此所求轨迹C的方程为y2=
 x-
x- .
.点评:本题重点考查抛物线的方程,考查抛物线的性质,考查韦达定理的运用,解题的关键是直线与抛物线联立,利用韦达定理解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其准线方程为
,其准线方程为