Question

已知抛物线C的一个焦点为F（，0），对应于这个焦点的准线方程为x=-.

（1）写出抛物线C的方程；

（2）过F点的直线与曲线C交于A、B两点，O点为坐标原点，求△AOB重心G的轨迹方程；

（3）点P是抛物线C上的动点，过点P作圆（x-3）²+y²=2的切线，切点分别是M，N.当P点在何处时，|MN|的值最小？求出|MN|的最小值.

Answer 1

（1）y²=2x.（2）y²= （3）当P点坐标为（2，±2）时，|MN|取最小值.

解析:

（1）抛物线方程为：y²=2x.           （4分）

（2）①当直线不垂直于x轴时，设方程为y=k(x-)，代入y²=2x，

得：k²x²-(k²+2)x+.

设A（x₁，y₁），B(x₂，y₂)，则x₁+x₂=，y₁+y₂=k(x₁+x₂-1)=.

设△AOB的重心为G（x，y）则，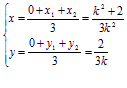

消去k得y²=为所求，                                            （6分）

②当直线垂直于x轴时，A（，1），B（，-1），                         （8分）

△AOB的重心G（，0）也满足上述方程.

综合①②得，所求的轨迹方程为y²=，                              （9分）

（3）设已知圆的圆心为Q（3，0），半径r=，

根据圆的性质有：|MN|=2.           （11分）

当|PQ|²最小时，|MN|取最小值，

设P点坐标为(x₀，y₀)，则y=2x₀.

|PQ|²=（x₀-3）²+ y= x-4x₀+9=(x₀-2)²+5，

∴当x₀=2，y₀=±2时，|PQ|²取最小值5，

故当P点坐标为（2，±2）时，|MN|取最小值.             （14分）