题目内容
如图,椭圆C: 的一个焦点为F(1,0),且过点(2,0).
的一个焦点为F(1,0),且过点(2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)若垂直于x轴的动直线与椭圆交于A,B两点,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.
 的一个焦点为F(1,0),且过点(2,0).
的一个焦点为F(1,0),且过点(2,0).(Ⅰ)求椭圆C的方程;
(Ⅱ)若垂直于x轴的动直线与椭圆交于A,B两点,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.

解:(Ⅰ)由题设,a=2,c=1,从而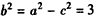 ,
,
所以,椭圆C的方程为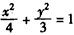 。
。
(Ⅱ)(ⅰ)由题意,得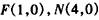 ,
,
设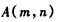 ,则
,则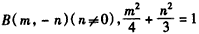 ,①
,①
AF与BN的方程分别为
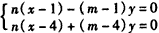 ,②
,②
设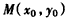 ,则有
,则有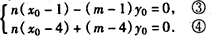
由③④,得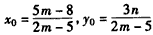 ,
,
由于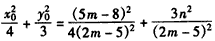
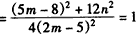 ,
,
所以,点M恒在椭圆C上。
(ⅱ)设AM的方程为x=ty+1,代入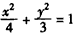 得
得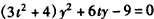 ,
,
设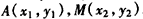 ,则有
,则有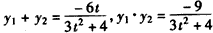 ,
,
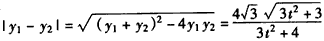 ,
,
令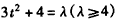 ,则
,则
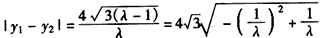
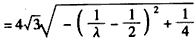 ,
,
因为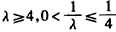 ,所以当
,所以当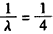 ,
,
即λ=4,t=0时,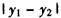 有最大值3,
有最大值3,
此时,△AMN的面积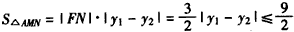 。
。
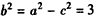 ,
,所以,椭圆C的方程为
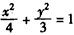 。
。(Ⅱ)(ⅰ)由题意,得
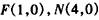 ,
,设
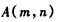 ,则
,则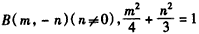 ,①
,①AF与BN的方程分别为
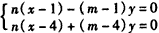 ,②
,②设
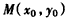 ,则有
,则有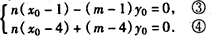
由③④,得
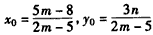 ,
,由于
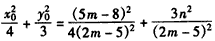
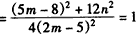 ,
,所以,点M恒在椭圆C上。
(ⅱ)设AM的方程为x=ty+1,代入
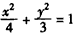 得
得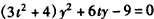 ,
,设
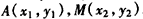 ,则有
,则有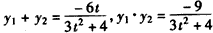 ,
,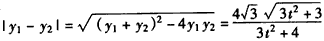 ,
,令
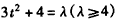 ,则
,则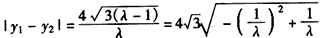
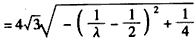 ,
,因为
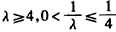 ,所以当
,所以当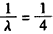 ,
,即λ=4,t=0时,
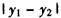 有最大值3,
有最大值3,此时,△AMN的面积
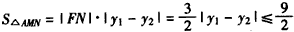 。
。
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
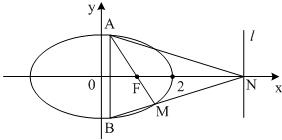 如图,椭圆C:
如图,椭圆C: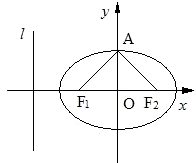 如图,椭圆C:
如图,椭圆C: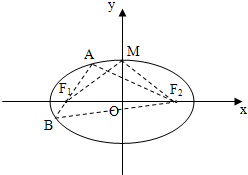 如图,椭圆C的中心在原点,焦点在x轴上,F1,F2分别是椭圆C的左、右焦点,M是椭圆短轴的一个端点,过F1的直线l与椭圆交于A,B两点,△MF1F2的面积为4,△ABF2的周长为
如图,椭圆C的中心在原点,焦点在x轴上,F1,F2分别是椭圆C的左、右焦点,M是椭圆短轴的一个端点,过F1的直线l与椭圆交于A,B两点,△MF1F2的面积为4,△ABF2的周长为 (2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:
(2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C: