Question

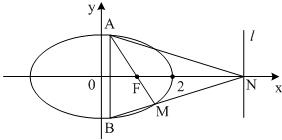如图，椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的一个焦点为F（1，0），且过点（2，0）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若AB为垂直于x轴的动弦，直线l：x=4与x轴交于点N，直线AF与BN交于点M．
（ⅰ）求证：点M恒在椭圆C上；
（ⅱ）求△AMN面积的最大值．

Answer 1

分析：（Ⅰ）由题设a=2，c=1，从而b²=a²-c²=3，即可得椭圆C前方程．
（Ⅱ）（i）由题意得F（1，0），N（4，0）．设A（m，n），则B（m，-n）（n≠0），

m2

4

+

n2

3

=1．
由题意知AF与BN的方程分别为：n（x-1）-（m-1）y=0，n（x-4）-（m-4）y=0．由此入手能够推出点M恒在椭圆G上．
（ⅱ）设AM的方程为x=ty+1，代入

x2

4

+

y2

3

=1得（3t²+4）y²+6ty-9=0．设A（x₁，y₁），M（x₂，y₂），利用根与系数的关系能够求出△AMN面积的最大值．

解答：解：
（Ⅰ）由题设a=2，c=1，从而b²=a²-c²=3，
所以椭圆C前方程为

x2

4

+

y2

3

=1．
（Ⅱ）（i）由题意得F（1，0），N（4，0）．
设A（m，n），则B（m，-n）（n≠0），

m2

4

+

n2

3

=1．①
AF与BN的方程分别为：n（x-1）-（m-1）y=0，
n（x-4）-（m-4）y=0．
设M（x₀，y₀），则有n（x₀-1）-（m-1）y₀=0，②
n（x₀-4）+（m-4）y₀=0，③
由②，③得
x₀=

5m-8

2m-5

，y0=

3n

2m-5

由于

x 2 0

4

+

y 2 0

3

=

(5m-8)2

4(2m-5)2

+

3n2

(2m-5)2

=

(5m-8)2

4(2m-5)2

+

3n2

(2m-5)2

=

(5m-8)2+12n2

4(2m-5)2

=

(5m-8)2+36-9m2

4(2m-5)2

=1
所以点M恒在椭圆G上．
（ⅱ）设AM的方程为x=ty+1，
代入

x2

4

+

y2

3

=1，得（3t²+4）y²+6ty-9=0．
设A（x₁，y₁），M（x₂，y₂），则有y1+y2 =-

6x

3x2+4

，y1y2=-

9

3t2+4

．
|y1-y2|  =

(y1+y2)2-4y1y2

=

4 3 • 3t2+3

3t2+4

，
令3t²+4=λ（λ≥4），则|y₁-y₂|=

4 3• λ-1

λ

=4

3

-( 1 λ )2+ 1 λ

=4

3

-( 1 λ - 1 2 ) 3+ 1 4

，
∵λ≥4，0＜

1

λ

≤

1

4

，∴当

1

λ

=

1

4

，即λ=4，t=0时，|y₁-y₂|有最大值3，此时AM过点F，△AMN的面积S△AMN=|FN||y1-y2|  =

3

2

|y1-y2|有最大值

9

2

．

点评：本题主要考查直线与椭圆的位置关系、轨迹方程、不等式等基本知识，考查运算能力和综合解题能力．