题目内容
(本小题10分)已知圆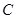 经过
经过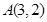 、
、 两点,且圆心在直线
两点,且圆心在直线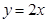 上.
上.
(1) 求圆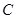 的方程;
的方程;
(2) 若直线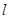 经过点
经过点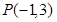 且与圆
且与圆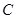 相切,求直线
相切,求直线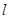 的方程.
的方程.
【答案】
(1)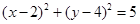 ;(2)
;(2)
【解析】本题考查用待定系数法求圆的方程以及直线方程的方法,体现了分类讨论的数学思想.
(1)设圆C的方程为(x-a)2+(y-b)2=r2,r>0,,依题意得: (3-a) 2+(2-b) 2=r2 ,(4-a) 2+(3-b) 2=r2
b=2a ,解出待定系数,可得圆 C的方程.
(2)当直线l的斜率存在时,可设直线l的方程,由圆心到直线的距离等于半径解出k值,从而得到直线l的方程.
解:(1)设圆的方程为

依题意得:
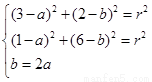
解得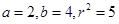
所以圆C的方程为 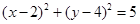
(2)由于直线L经过点(-1,3),故可设直线L的方程为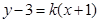
即: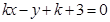
因为直线L与圆C相切,且圆C的圆心为(2,4),半径为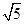 所以有
所以有
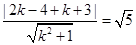
解得k=2或k= - 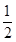
所以直线L的方程为即:


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,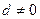 ,
,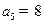 ,且项
,且项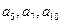 分别是某一等比数列
分别是某一等比数列 中的第
中的第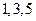 项,(1)求数列
项,(1)求数列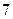 项。
项。
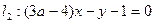 且
且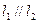 ,求以N(1,1)为圆心,并且与
,求以N(1,1)为圆心,并且与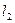 相切的圆的方程.
相切的圆的方程.
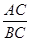 的值.
的值. ,
, ;
; .
.