题目内容
下列四个命题:
①直线 与圆
与圆 恒有公共点;
恒有公共点;
② 为△ABC的内角,则
为△ABC的内角,则 最小值为
最小值为 ;
;
③已知a,b是两条异面直线,则过空间任意一点P都能作并且只能作一条直线与a,b都垂直;
④等差数列{ }中,
}中, 则使其前n项和
则使其前n项和 成立的最大正整数为2013;
成立的最大正整数为2013;
其中正确命题的序号为 。(将你认为正确的命题的序号都填上)
【答案】
(1)(3)
【解析】
试题分析:①中,圆心(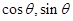 )到直线
)到直线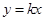 的距离为
的距离为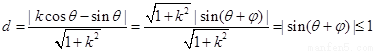 ,所以直线与圆恒有公共点,正确;
,所以直线与圆恒有公共点,正确;
②中,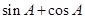 =
=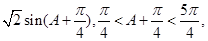 所以②不正确;
所以②不正确;
③中,根据异面直线所成的角的定义及直线的平移,异面直线的公垂线唯一,③正确;
④中,∵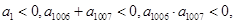
∴a1006和a1007异号∴a1006<0,a1007>0,
∵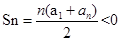 ,∴a1+an<0
,∴a1+an<0
∴a1006+a1007<0,
∵a1006+a1007=a1+a2012,
∴a1+a2013<0,∴n最大为2012,④不正确。故答案为(1)(3).
考点:本题主要考查直线与圆的位置关系,三角函数和角公式,异面直线的关系,等差数列的求和公式。
点评:中档题,本题综合性较强,考查知识点涉及直线与圆的位置关系,三角函数和角公式,异面直线的关系,等差数列的求和公式。三角函数的图象和性质。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
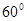 的菱形
的菱形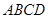 沿较短对角线
沿较短对角线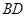 折成二面角
折成二面角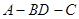 ,点
,点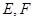 分别为
分别为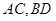 的中点,给出下列四个命题:
的中点,给出下列四个命题: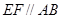 ;②
;②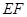 是异面直线
是异面直线 与
与 ;④
;④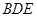 .
.