题目内容
设P为曲线C：y=x2+2x+3上的点，且曲线C在点P处切线倾斜角的取值范围为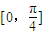
，则点P纵坐标的取值范围为（ ）A．
B．
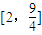
C．[2，3]
D．[2，6]
【答案】分析：切线的斜率k=tanθ∈[0，1]．设切点为P（x，y），k=y′|x=x0=2x+2，上此可知点P横坐标的取值范围．
解答：解：∵切线的斜率k=tanθ∈[tan0，tan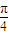
]=[0，1]．
设切点为P（x，y），于是k=y′|x=x0=2x+2，
∴x∈[-1，-
]
则y∈[2，
]．
故选B．
点评：本题考查圆锥曲线的基本性质和应用，同时考查了二次函数在给定区间上的值域，解题时要认真审题，仔细解答．
解答：解：∵切线的斜率k=tanθ∈[tan0，tan
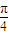]=[0，1]．设切点为P（x，y），于是k=y′|x=x0=2x+2，
∴x∈[-1，-
]则y∈[2，
]．故选B．
点评：本题考查圆锥曲线的基本性质和应用，同时考查了二次函数在给定区间上的值域，解题时要认真审题，仔细解答．
练习册系列答案
相关题目