题目内容
已知f(x)=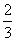 x3-2x2+cx+4,g(x)=ex-e2-x+f(x),
x3-2x2+cx+4,g(x)=ex-e2-x+f(x),
(1)若f(x)在x=1+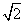 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;
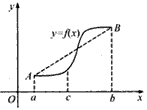
(2)如下图所示,若函数y=f(x)的图象在[a,b]上连续光滑,试猜想拉格朗日中值定理:即一定存在c∈(a,b)使得f′(c)=?[用含有a,b,f(a),f(b)的表达方式直接回答,不需要写猜想过程]
(3)利用(2)证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4。
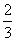 x3-2x2+cx+4,g(x)=ex-e2-x+f(x),
x3-2x2+cx+4,g(x)=ex-e2-x+f(x),(1)若f(x)在x=1+
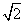 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;(2)如下图所示,若函数y=f(x)的图象在[a,b]上连续光滑,试猜想拉格朗日中值定理:即一定存在c∈(a,b)使得f′(c)=?[用含有a,b,f(a),f(b)的表达方式直接回答,不需要写猜想过程]
(3)利用(2)证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4。
解:(1)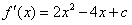 ,依题意有
,依题意有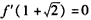 ,
,
即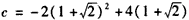 =-2,
=-2,
∴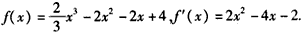 ,
,
令f′(x)>0,得 或
或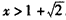 ,
,
从而f(x)的单调增区间为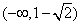 或
或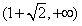 。
。
(2)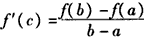 ;
;
(3)由已知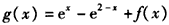
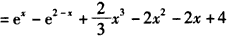 ,
,
所以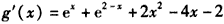 ,
,
 =2e-4,
=2e-4,
由(2)知,对于函数y=g(x)图象上任意两点A,B,
在A,B之间一定存在一点C(c,g(c)),使得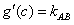 ,
,
又g′(x)≥2e-4,故有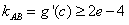 ,证毕。
,证毕。
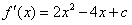 ,依题意有
,依题意有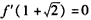 ,
,即
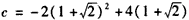 =-2,
=-2,∴
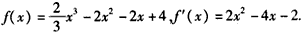 ,
,令f′(x)>0,得
 或
或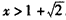 ,
,从而f(x)的单调增区间为
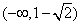 或
或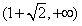 。
。 (2)
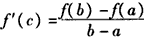 ;
;(3)由已知
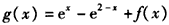
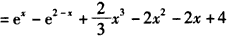 ,
,所以
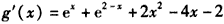 ,
, =2e-4,
=2e-4,由(2)知,对于函数y=g(x)图象上任意两点A,B,
在A,B之间一定存在一点C(c,g(c)),使得
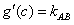 ,
,又g′(x)≥2e-4,故有
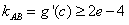 ,证毕。
,证毕。 
练习册系列答案
相关题目