题目内容
已知f(x)=-x3+ax2-4
,f′(x)是f(x)的导函数.
(1)当a=2时,求函数f(x)的单调区间;
(2)当a=2时,对任意的m∈[-1,1],n∈[-1,1],求f(m)+f'(n)的最小值;
(3)若?x0∈(0,+∞),使f(x)>0,求a取值范围.
|
(1)当a=2时,求函数f(x)的单调区间;
(2)当a=2时,对任意的m∈[-1,1],n∈[-1,1],求f(m)+f'(n)的最小值;
(3)若?x0∈(0,+∞),使f(x)>0,求a取值范围.
分析:(1)由题意知f(x)=-x3+2x2-4,f′(x)=-3x2+4x,由导数解出函数的单调区间即可;
(2)可分别求f(m)、f′(n)的最小值,再求f(m)+f′(n)的最小值,
(2)存在x0∈(0,+∞),使f(x0)>0即寻找f(x)max>0的变量a的范围.由此知可先求函数函数在(0,+∞)上的最大值,再令最大值大于0即可得到关于a的不等式,解此不等式求出它的取值范围
(2)可分别求f(m)、f′(n)的最小值,再求f(m)+f′(n)的最小值,
(2)存在x0∈(0,+∞),使f(x0)>0即寻找f(x)max>0的变量a的范围.由此知可先求函数函数在(0,+∞)上的最大值,再令最大值大于0即可得到关于a的不等式,解此不等式求出它的取值范围
解答:解:(1)由题意知f(x)=-x3+2x2-4,f′(x)=-3x2+4x
令f′(x)=0,得x=0或
令f′(x)>0,可解得x∈(0,
),令f′(x)<0,可解得x∈(-∞,0)∪(
,+∞),
故函数在x∈(0,
)上是增函数,在(-∞,0)与(
,+∞)上是减函数,
(2)由(1)知
当x在[-1,1]上变化时,f(x),f′(x)随x的变化情况如下表:
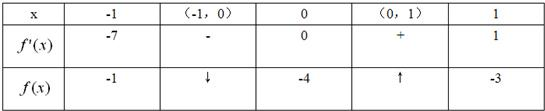
∴对于m∈[-1,1],f(m)的最小值为f(0)=-4,
∵f′(x)=-3x2+4x的对称轴为 x =
且抛物线开口向下
∴对于n∈[-1,1],f′(n)的最小值为f′(-1)=-7,
∴f(m)+f′(n)的最小值为-11.
(2)∵f′(x)=-3x(x-
)
①若a≤0,当x>0,时f′(x)<0
∴f(x)在[0,+∞)上单调递减,又f(0)=-4,则当x>0时,f(x)<-4∴当a≤0时,不存在x0>0,使f(x0)>0
②若a>0,则当0<x<
时,f′(x)>0,
当x>
时,f′(x)<0从而f(x)在(0,
]上单调递增,在[
,+∞)上单调递减,
∴当x∈(0,+∞)时,f(x)max=f(
)=-
+
-4
根据题意,
-4>0,即a3>27,解得a>3
综上,a的取值范围是(3,+∞)
令f′(x)=0,得x=0或
| 4 |
| 3 |
令f′(x)>0,可解得x∈(0,
| 4 |
| 3 |
| 4 |
| 3 |
故函数在x∈(0,
| 4 |
| 3 |
| 4 |
| 3 |
(2)由(1)知
当x在[-1,1]上变化时,f(x),f′(x)随x的变化情况如下表:

∴对于m∈[-1,1],f(m)的最小值为f(0)=-4,
∵f′(x)=-3x2+4x的对称轴为 x =
| 2 |
| 3 |
∴对于n∈[-1,1],f′(n)的最小值为f′(-1)=-7,
∴f(m)+f′(n)的最小值为-11.
(2)∵f′(x)=-3x(x-
| 2a |
| 3 |
①若a≤0,当x>0,时f′(x)<0
∴f(x)在[0,+∞)上单调递减,又f(0)=-4,则当x>0时,f(x)<-4∴当a≤0时,不存在x0>0,使f(x0)>0
②若a>0,则当0<x<
| 2a |
| 3 |
当x>
| 2a |
| 3 |
| 2 |
| 3 |
| 2a |
| 3 |
∴当x∈(0,+∞)时,f(x)max=f(
| 2a |
| 3 |
| 8a3 |
| 27 |
| 4a2 |
| 9 |
根据题意,
| 4a3 |
| 27 |
综上,a的取值范围是(3,+∞)
点评:本题考查利用求函数单调区间,求函数的最值,及函数恒成立问题的求解,转化的思想及推理判断的能力,解题的关键是熟练掌握导数的运算,利用导数研究函数的性质的方法,本题运算量较大,易出错,解题时要严谨认真,

练习册系列答案
相关题目