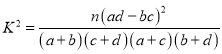题目内容
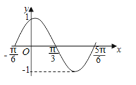
【题目】如图是函数
在区间
上的图象，为了得到这个函数的图象，只需将
的图象上的所有点（ ）
A.向左平移
个长度单位，再把所得各点的横坐标变为原来的
，纵坐标不变
B.向左平移个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变
C.向左平移
个长度单位，再把所得各点的横坐标变为原来的，纵坐标不变
D.向左平移个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变
【答案】A
【解析】
首先根据函数的周期和振幅确定
和
的值，再代入特殊点可确定
的一个值，进而得到函数的解析式，再进行平移变换即可.
由图像可知函数的周期为
，振幅为
，
所以函数的表达式可以是
，
代入
可得的一个值为
，
故函数中的一个表达式是
，即 
，
所以只需将
的图像上的所有点
向左平移个长度单位，再把所得各点的横坐标变为原来的
，纵坐标不变.
故选：A
练习册系列答案
优质课堂快乐成长系列答案
相关题目
【题目】某学校为了解学生假期参与志愿服务活动的情况，随机调查了
名男生，名女生，得到他们一周参与志愿服务活动时间的统计数据如右表（单位：人）：
超过 | 不超过 | |
男 |
|
|
女 |
|
|
（1）能否有
的把握认为该校学生一周参与志愿服务活动时间是否超过
小时与性别有关？
（2）以这
名学生参与志愿服务活动时间超过小时的频率作为该事件发生的概率，现从该校学生中随机抽查
名学生，试估计这名学生中一周参与志愿服务活动时间超过小时的人数.
附：
|
|
|
|
|
|
|
|
