题目内容
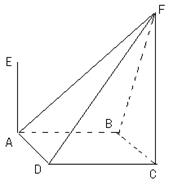
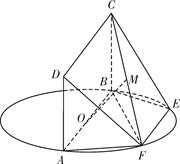
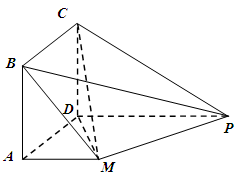
如图,在三棱锥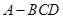 中,
中, ,
, ,
, ,设顶点A在底面
,设顶点A在底面 上的射影为R.
上的射影为R.
(Ⅰ)求证: 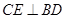 ;
;
(Ⅱ)设点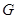 在棱
在棱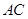 上,且
上,且 ,试求二面角
,试求二面角 的余弦值.
的余弦值.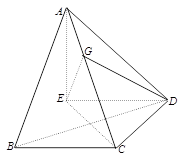
(Ⅰ)见解析;(Ⅱ)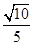 .
.
解析试题分析:(Ⅰ)借助几何体的中线面垂直,证明BCDE为正方形,达到证明线线垂直的目的;(Ⅱ)方法一利用定义法做出二面角,通过解三角形求解二面角的平面角;方法二建立利用空间向量法,通过两个半平面的法向量借助夹角公式求解.
试题解析:证明:方法一:由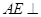 平面
平面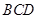 ,得
,得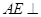
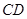 ,
,
又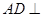
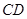 ,则
,则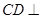 平面
平面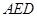 ,
,
故 , 3分
, 3分
同理可得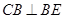 ,则
,则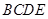 为矩形,
为矩形,
又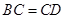 ,则
,则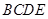 为正方形,故
为正方形,故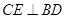 . 5分
. 5分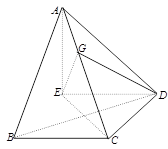
方法二:由已知可得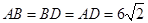 ,设
,设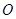 为
为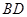 的中点,则
的中点,则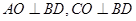 ,则
,则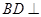 平面
平面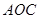 ,故平面
,故平面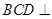 平面
平面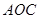 ,则顶点
,则顶点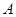 在底面
在底面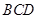 上的射影
上的射影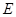 必在
必在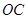 ,故
,故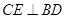 .
.
(Ⅱ)方法一:由(I)的证明过程知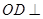 平面
平面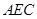 ,过
,过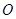 作
作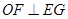 ,垂足为
,垂足为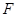 ,则易证得
,则易证得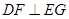 ,故
,故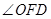 即为二面角
即为二面角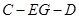 的平面角, 8分
的平面角, 8分
由已知可得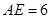 ,则
,则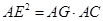 ,故
,故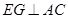 ,则
,则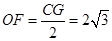 ,
,
又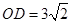 ,则
,则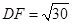 , 10分
, 10分
故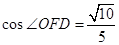 ,即二面角
,即二面角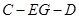 的余弦值为
的余弦值为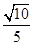 12分
12分
方法二: 由(I)的证明过程知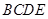 为正方形,如图建立坐标系,
为正方形,如图建立坐标系,
则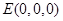 ,
,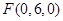
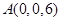 ,
,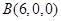
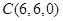 ,可得
,可得 , 8分
, 8分
则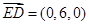 ,
,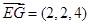 ,易知平面
,易知平面
的一个法向量为 ,设平面
,设平面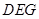 的一个法向量为
的一个法向量为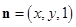 ,则由
,则由 得
得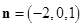 10分
10分
则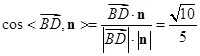 ,即二面角
,即二面角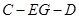 的余弦值为
的余弦值为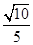 . 12分
. 12分
考点:1.垂直关系的证明;2.二面角;3.空间向量.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
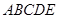 中,
中, 平面
平面 ,
,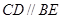 ,
,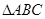 是等腰直角三角形,
是等腰直角三角形,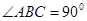 ,且
,且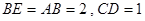 ,点
,点 是
是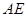 的中点.
的中点.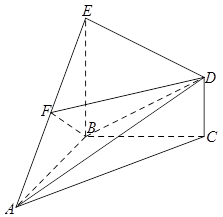
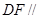 平面
平面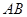 与平面
与平面 所成角的正弦值.
所成角的正弦值. 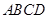 是正方形,
是正方形,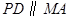 ,
,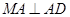 ,
, ,
, 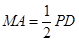 .
.
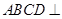 平面
平面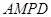 ;
;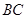 与
与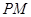 所成的角为
所成的角为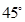 ,求二面角
,求二面角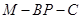 的余弦值.
的余弦值.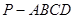 中,
中,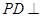 底面
底面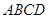 ,面
,面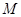 为侧棱
为侧棱 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示. 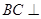 平面
平面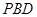 ;
; 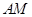 ∥平面
∥平面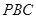 ;
; 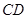 上是否存在点
上是否存在点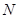 ,使
,使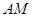 与
与 所成角的余弦值为
所成角的余弦值为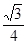 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点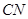 的长;若不存在,说明理由.
的长;若不存在,说明理由.
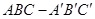 的侧棱长为3,
的侧棱长为3,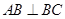 ,且
,且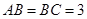 ,
,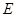 、
、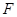 分别是棱
分别是棱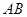 、
、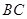 上的动点,且
上的动点,且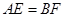
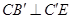 ;
;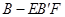 .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线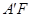 与
与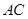 所成角的余弦值.
所成角的余弦值.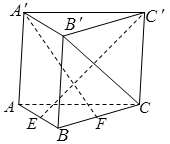
 ,AE、CF都与平面ABCD垂直,AE=1,CF=2.
,AE、CF都与平面ABCD垂直,AE=1,CF=2.