题目内容
抛物线y2=4x的焦点为F,准线l交x轴于R点,过抛物线上一点P(4,4)作PQ⊥l于Q,则梯形PQRF的面积为
- A.12
- B.14
- C.16
- D.18
B
分析:求梯形PQRF的面积,关键是确定梯形的上底,下底,及高的长,利用抛物线的定义即可求得.
解答:∵抛物线方程为y2=4x,焦点为F,准线l交x轴于R点
∴抛物线的准线方程为:x=-1,FR=2
∵过抛物线上一点P(4,4)作PQ⊥L于Q
∴|QR|=4,|PQ|=5
∴梯形PQRF的面积为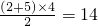
故选B.
点评:本题考查梯形的面积,解题的关键是利用抛物线的几何性质,正确运用梯形的面积公式.
分析:求梯形PQRF的面积,关键是确定梯形的上底,下底,及高的长,利用抛物线的定义即可求得.
解答:∵抛物线方程为y2=4x,焦点为F,准线l交x轴于R点
∴抛物线的准线方程为:x=-1,FR=2
∵过抛物线上一点P(4,4)作PQ⊥L于Q
∴|QR|=4,|PQ|=5
∴梯形PQRF的面积为
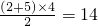
故选B.
点评:本题考查梯形的面积,解题的关键是利用抛物线的几何性质,正确运用梯形的面积公式.

练习册系列答案
相关题目